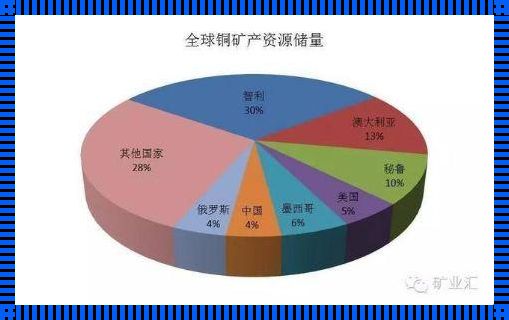
中国必须要进口的资源
在经济全球化的大背景下,我国与世界各国之间的贸易往来日益密切,对各种资源的进口需求也日益增加。这其中,有几种资源是我国必须要依赖进口的。能源作为现代社会经济发展的命脉,能源的需求量巨大。尽管我国在能源领域的开发已经取得了显著的成果,但国内石油、天然气的产量仍远不能满足我国的需求,因此,我国必须
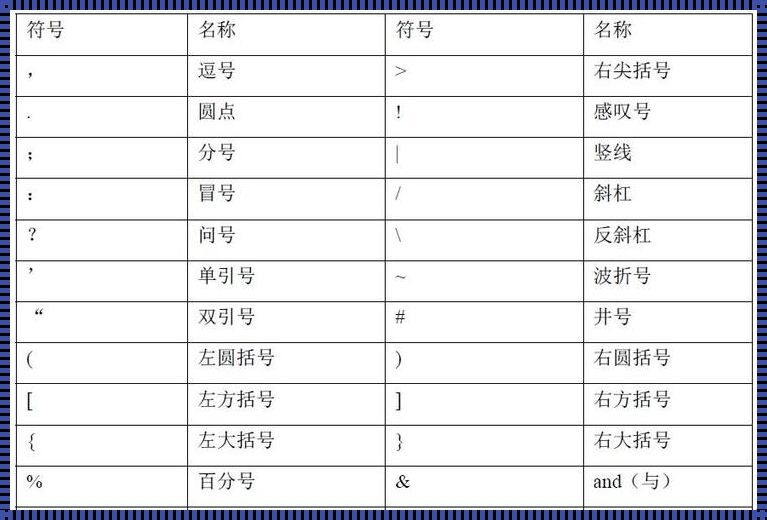
C语言符号的奥秘之门 - 探索程式代码灵魂
C语言,作为一种经典的编程语言,其简洁、高效的特点一直受到广大程序员的喜爱。而C语言的魅力,很大程度上来自于其独特的符号系统。这些符号,如同搭建起一座座沟通现实与虚拟世界的桥梁,使得我们可以通过它们来操控计算机,实现我们的想法和创意。揭开基本符号的面纱,我们可以看到加号(+)、减号(-)、乘号(
网线,对称线的奥秘
在现代社会,网络已经成为了我们生活中不可或缺的一部分。而连接网络的桥梁,就是那细小的网线。但是,你是否想过,网线究竟是不是对称线呢?今天,就让我们一起揭开这个谜题的神秘面纱。一、对称线的定义在对称线这个词中,包含了两个重要的信息:信号传输和导线。而对称线,就是指那些在传输信号时,具有相同的传输
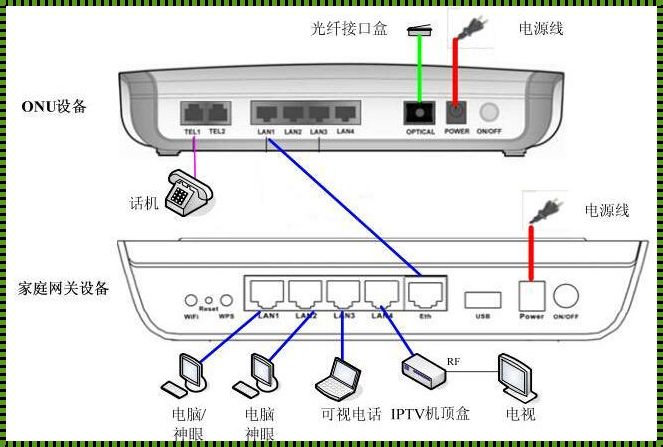
宽带机顶盒安装教程:开启家庭娱乐新篇章
宽带机顶盒正成为现代家庭娱乐的重要组成部分。它能够将互联网、数字电视和各种流媒体服务汇集在一个设备中。无论你是想观看电影、电视节目、玩游戏还是上网,宽带机顶盒都能满足你的需求。在开始安装之前,请确保你有以下物品:宽带机顶盒、电源线、HDMI线或AV线、遥控器、电池。如果这是你第一次安装宽带机顶盒
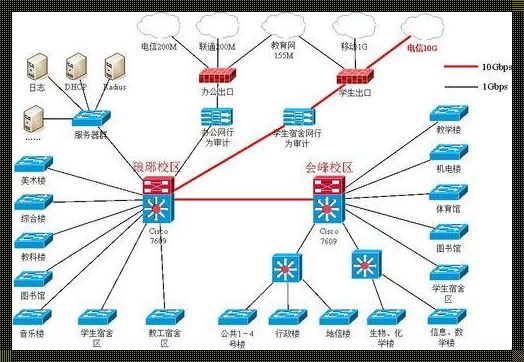
总线型拓扑:计算机网络的坚实骨架
在计算机网络的世界里,总线型拓扑就像是一座桥梁,将所有的设备紧密地联系在一起。它以一种独特的方式,让每一个设备都能与其他设备进行通信,从而构建起一个完整的网络世界。总线型拓扑,顾名思义,就是将所有的设备都连接到一个共同的传输介质上。这个介质就像是一条长长的街道,所有的设备就像是街道两旁的建筑,它
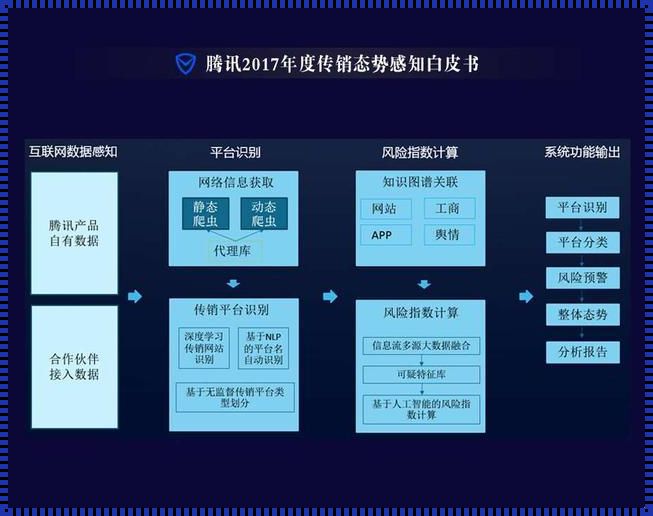
腾讯白皮书事件:互联网巨头背后的反思
作为一名互联网行业的从业人员,我有幸亲身经历了腾讯白皮书事件的始末。这场风波从一开始就引起了广泛关注,并迅速成为网络上的热点话题。事件的爆发,不仅让腾讯的公众形象受到了影响,也让我们重新审视了互联网巨头在当下社会中的作用和责任。起初,当腾讯白皮书事件被曝光时,我感到非常震惊。我无法相信,一家一直
《深入探讨if语句的嵌套极限》
在程序设计的海洋中,我们常常需要借助各种控制流语句来引导程序的航向。其中,if语句就像是一只不可或缺的罗盘,帮助我们根据不同的条件来决定程序的行进路线。然而,就像海洋中暗礁重重,if语句的嵌套使用也存在着不可忽视的极限。我们可能会好奇,if语句到底可以嵌套多少层?这实际上取决于我们所使用的编程语
安卓应用备份成APK的惊人发现
随着智能手机的普及,安卓操作系统成为了市场上的主流之一。对于许多用户来说,安卓设备上的各种应用程序是日常生活和工作不可或缺的一部分。然而,当涉及到应用程序的备份问题时,许多人可能会感到困惑和担忧。最近,我在尝试将安卓应用备份成APK的过程中,有了一些惊人的发现。首先,我发现并非所有的安卓应用都支
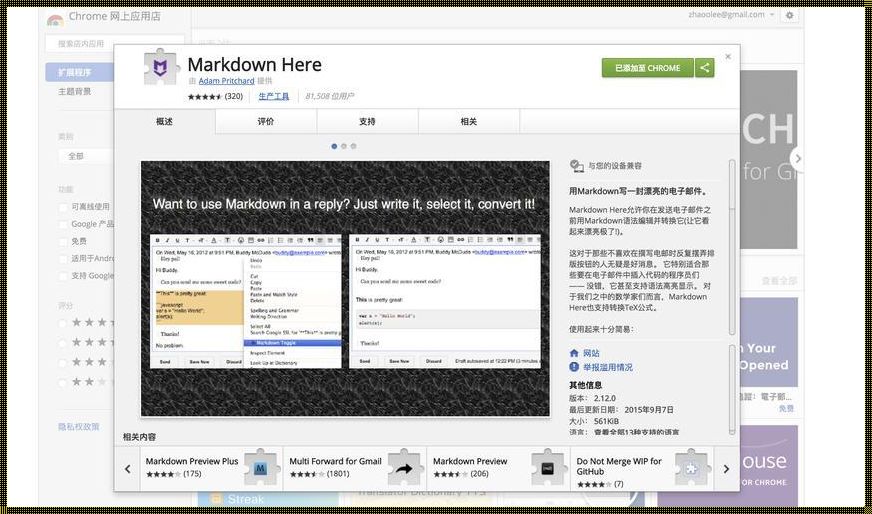
Markdown文本编辑器:简约书写的奥义
作为一名热爱文字的人,我一直渴望找到一种能够提升写作效率并带来愉悦感的工具。在一次偶然的机会中,我发现了Markdown文本编辑器。这款编辑器以其简洁的语法和强大的功能,立刻吸引了我的注意。从那时起,Markdown文本编辑器便成为了我不可或缺的写作伙伴。Markdown文本编辑器的一大特色在于
扩展欧几里得求逆元:逆元之谜的破解之旅
引言在数学的世界中,逆元一直是一个令人着迷的概念。那么,什么是逆元?逆元在数学中的意义是什么?为了回答这个问题,我们需要深入探讨扩展欧几里得算法。逆元的定义及其在数学中的意义逆元,顾名思义,就是一个数与其倒数互为倒数。在数学中,逆元通常用于解决线性方程组。设$a$和$b$是互质的正整数,那么