完全图K4是什么：对图论中的这一概念进行深入探讨与研究
在图论的海洋中，完全图K4就像一颗璀璨的明珠，吸引着无数数学家和学者的目光。那么，完全图K4究竟是什么呢？它有何特殊之处，又为何在图论中占有如此重要的地位呢？首先，让我们从基础的概念入手。图论，简单来说，就是研究图的性质和规律的数学分支。而图，就是由点集合及连接这些点的边集合组成的数学结构。在这
“分数家长版app下载”盛典：一场教育科技的狂欢
我，作为一名家长，对孩子的教育始终怀着深深的期待和关注。有一天，我在朋友的推荐下，下载了“分数家长版app”。从此，我的生活多了一份期待，期待孩子在分数的引领下，走向更广阔的知识天地。这个app，对我来说，就像一个神秘的宝盒，里面装满了教育的智慧和科技的便利。我可以随时随地了解孩子的学习情况，可
王翡瑜创业：用知识开启梦想之旅
在这个充满变革与机遇的时代，越来越多的人选择创业，用他们的智慧和勇气书写属于自己的传奇。王翡瑜，一个充满激情与智慧的年轻人，也踏上了这片广阔的创业天地。他坚信，知识就是力量，而他的梦想之旅，就从这里开始。王翡瑜从小就对知识有着极大的渴望，他热爱学习，善于思考，始终保持着对新事物的好奇心。在他看来
![揭开神秘面纱：Word参考文献标注[1]的技巧与艺术](http://yuguangkj.cn/zb_users/upload/2024/01/20240106001117_57126.jpg "揭开神秘面纱：Word参考文献标注[1]的技巧与艺术")
揭开神秘面纱：Word参考文献标注[1]的技巧与艺术
在学术写作的海洋中，Word参考文献标注[1]就像是一盏指路的灯塔，它不仅为我们的研究提供了丰富的资料支持，更是我们学术道路上不可或缺的伙伴。然而，对于许多初学者来说，它仍笼罩在一层神秘的面纱之下。今天，就让我们一起揭开这层神秘的面纱，探索Word参考文献标注[1]的技巧与艺术。首先，让我们从最
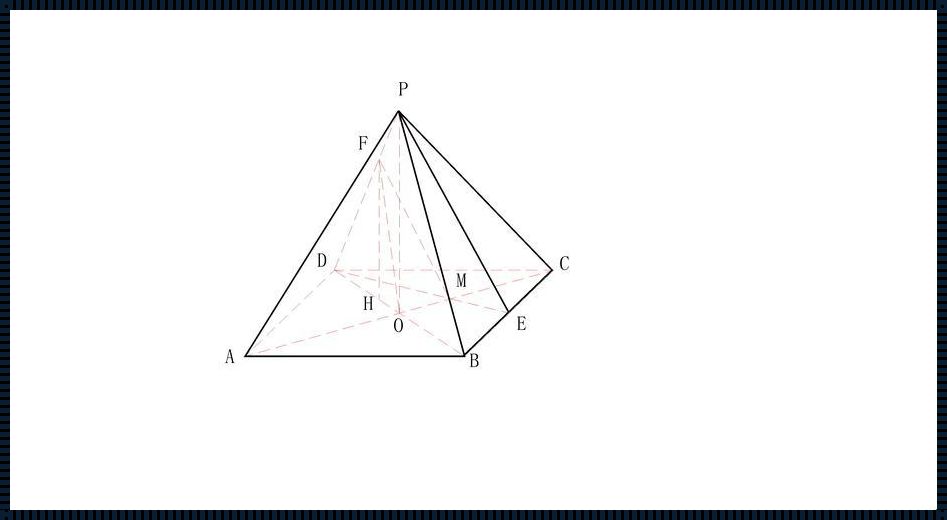
四棱锥底面一定是什么形——揭秘四棱锥底面的奥秘
在几何学中，四棱锥是一种常见的立体几何图形，它由一个四边形的底面和一个顶点组成。然而，四棱锥底面一定是什么形呢？这就是我们今天要探讨的问题。首先，我们需要明确四棱锥的定义。四棱锥是一种立体几何图形，它的底面是一个四边形，而侧面是由底面的四个顶点与顶点相连形成的三角形。因此，四棱锥的底面一定是一个
惊现云朵形状的符号：意义与象征的深度解析
在人类历史长河中，符号一直是传递信息、表达情感、记录历史的重要载体。从古至今，各种各样的符号层出不穷，其中，云朵形状的符号尤为引人注目。这个看似简单，实则充满深意的符号，究竟隐藏着怎样的奥秘呢？首先，云朵形状的符号代表着自然界的云。云是天空的诗人，是大自然的画家，它以千变万化的姿态，装点着我们的
回文诗最短的一首诗：一箭双雕的艺术魅力
独坐孤舟观月，江水东流，月影西斜，一箭双雕，这是回文诗最短的一首诗。这首诗的魅力在于其独特的艺术表现形式，仅用十个字就描绘出一幅美丽的江月图。接下来，我将从不同的角度对这首诗进行剖析，展示其艺术魅力。首先，从语言的角度来看，这首诗采用了简洁明了的文字，既描绘了江水的流动，又展现了月影的倾斜，同时
房间扫描摄像头：震惊科技与隐私的边界
在一个宁静的夜晚，我独自坐在书桌前，灯光下，一台小小的房间扫描摄像头静静地立在那里，它的存在，让我感到震惊。我无法忽视这个小小的设备，它似乎在默默诉说着一个关于科技与隐私边界的复杂故事。我拿起摄像头，仔细端详。它小巧，精致，黑色的外壳，红色的指示灯，静静地注视着这个小小的空间。我无法想象，这样一
hacs无法访问github，问题究竟出在哪里？
作为一款智能家居的必备利器，HACS（HomeAssistantCommunityStore）一直备受广大用户的喜爱。然而，近期有不少用户反映，HACS无法访问GitHub，这无疑给用户带来了不小的困扰。那么，这个问题究竟出在哪里呢？首先，我们需要了解HACS的运作原理。HACS是一个基于
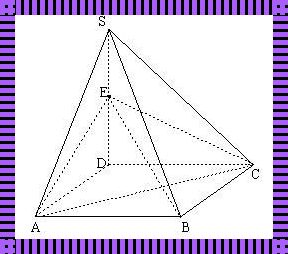
正四棱锥的底面是正方形吗？——深入剖析与探讨
在我们的日常生活中，正四棱锥这个几何形状并不常见，但在数学和工程领域，它却扮演着重要的角色。那么，正四棱锥的底面是否是正方形呢？这个问题看似简单，实则需要我们进行深入的剖析和探讨。首先，我们需要明确正四棱锥的定义。正四棱锥是一种四棱锥，其底面为正方形，侧面为等腰三角形。根据这个定义，我们可以得出
