在统计学中，皮尔逊相关系数和斯皮尔曼等级相关系数是两种常用的衡量变量间线性关系的方法。它们各自有着不同的应用场景和优缺点。

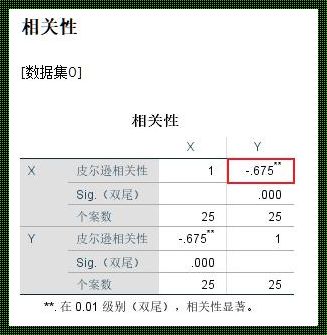
一、皮尔逊相关系数的优点

皮尔逊相关系数是一种衡量两个变量间线性关系强度和方向的指标。其优点如下：

• 适用性强：皮尔逊相关系数适用于连续变量，并且对数据的分布形态没有特殊要求。
• 计算简便：皮尔逊相关系数的计算公式较为简单，易于理解和编程实现。
• 结果直观：皮尔逊相关系数的值介于-1和1之间，可以直接反映变量间的线性关系强度和方向。

二、皮尔逊相关系数的缺点

然而，皮尔逊相关系数也存在一些局限性：

• 对非正态分布数据敏感：当数据偏离正态分布较远时，皮尔逊相关系数的估计可能会受到影响。
• 不适用于非线性关系：皮尔逊相关系数只能衡量变量间的线性关系，对于非线性关系则无法有效捕捉。
• 对异常值敏感：皮尔逊相关系数对异常值较为敏感，异常值的存在可能会影响相关系数的估计。

三、斯皮尔曼相关系数的优点

斯皮尔曼等级相关系数则是另一种衡量变量间关系的方法，它通过将原始数据转换为等级，从而避免了数据分布和异常值的影响。其优点包括：

• 对异常值不敏感：由于斯皮尔曼相关系数是基于等级计算，因此它对异常值不敏感。
• 适用于非正态分布数据：斯皮尔曼相关系数不要求数据服从正态分布，因此在实际应用中具有更广泛的适用性。
• 可处理非线性关系：虽然斯皮尔曼相关系数主要用于衡量线性关系，但它在一定程度上也能捕捉非线性关系。

四、斯皮尔曼相关系数的缺点

然而，斯皮尔曼相关系数也有其不足之处：

• 精度较低：由于斯皮尔曼相关系数是通过等级计算，因此其精度相对较低，不如皮尔逊相关系数精确。
• 无法直接反映变量间的关系强度：斯皮尔曼相关系数的值介于-1和1之间，但其绝对值的大小并不能直接反映变量间的真实关系强度。

五、结论

综上所述，皮尔逊相关系数和斯皮尔曼相关系数各有优缺点。在实际应用中，应根据数据的特点和研究需求选择合适的指标。例如，当数据分布较为规范且需要较高精度时，可以选择皮尔逊相关系数；而当数据中存在异常值或非正态分布时，可以考虑使用斯皮尔曼相关系数。