随着科技的飞速发展，数据分析在各个领域发挥着越来越重要的作用。在众多统计学中，威布尔分布作为一种具有广泛应用背景的概率分布，逐渐引起了人们的广泛关注。本文将带您走进威布尔分布的世界，探讨其背后的数学之美以及在现实中的应用。

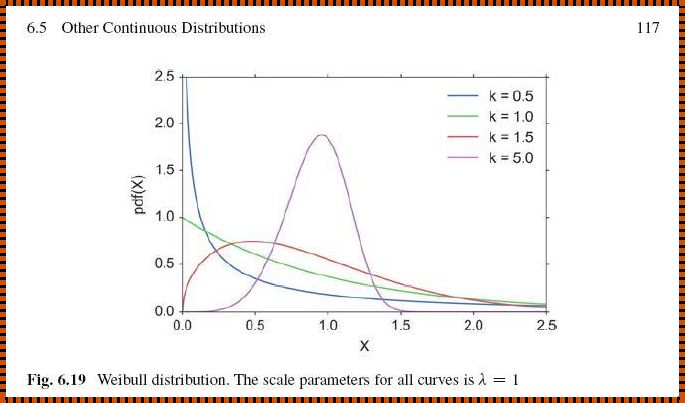
一、威布尔分布概述

威布尔分布是一种连续概率分布，由瑞典工程师 Waloddi Weibull 在1939年首次提出。它被广泛应用于可靠性分析、生存分析、材料科学等领域。威布尔分布的形状可以通过两个参数进行调整，即形状参数 k 和尺度参数 lambda (λ)。当 k=1 时，威布尔分布退化为指数分布；当 k>1 时，威布尔分布呈现出更复杂的形状，可用于描述多种不同的数据特征。

二、威布尔分布在数学中的美

威布尔分布的美在于其灵活性和普适性。它可以模拟多种不同类型的失效模式，如突然失效、渐变失效以及混合失效等。此外，威布尔分布还具有可加性和可分解性，这使得它在处理复杂系统时具有很大的优势。通过引入威布尔分布，我们可以更好地理解和预测各种现象的发生规律，从而为实际问题的解决提供有力的数学工具。

三、威布尔分布在现实中的应用

威布尔分布在现实中的应用非常广泛，以下是一些典型的应用场景：

1. 可靠性分析：在工程领域，威布尔分布常用于评估设备的可靠性。通过对设备的使用寿命数据进行威布尔分布拟合，可以预测设备的平均无故障运行时间（MTBF），从而为设备的维护和更换提供决策依据。

2. 生存分析：在医学领域，威布尔分布被用于研究患者的生存时间。通过对患者生存数据的威布尔分布拟合，可以预测患者的平均生存时间，从而为治疗方案的选择提供参考。

3. 材料科学：在材料科学领域，威布尔分布被用于描述材料的疲劳寿命。通过对材料的疲劳寿命数据进行威布尔分布拟合，可以预测材料的平均疲劳寿命，从而为材料的选用和设计提供指导。

四、结语

威布尔分布作为一种具有广泛应用背景的概率分布，其背后的数学之美以及在现实中的应用值得我们深入研究和探讨。通过对威布尔分布的学习和应用，我们可以更好地理解各种现象的发生规律，为解决实际问题提供有力的数学工具。让我们共同探索威布尔分布的神秘世界，揭示其背后的数学之美与现实应用！