你是否曾经思考过，为什么伽马分布相除会得到贝塔分布？这个问题听起来可能有些抽象，但它的背后隐藏着深刻的数学原理和实际应用。

一、伽马分布与贝塔分布的渊源

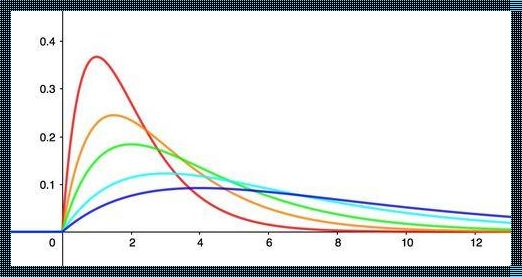
伽马分布，作为统计学中的一种重要分布，广泛应用于寿命分析、可靠性理论等领域。而贝塔分布，则常用于描述定量的比例数据，如生物学中的种群比例、金融中的风险敞口比例等。这两个分布看似风马牛不相及，但在数学家们的眼中，它们却有着千丝万缕的联系。

伽马分布相除为贝塔，这并非是一个简单的操作，而是一个蕴含着深刻数学意义的变换。这种变换不仅揭示了两种分布之间的内在联系，还为我们在解决实际问题提供了新的视角和方法。

二、伽马分布相除为贝塔的数学原理

伽马分布是一种连续概率分布，其概率密度函数由两个参数决定：形状参数k和尺度参数θ。当我们对两个独立的伽马随机变量进行除法运算时，结果将服从一个新的分布——贝塔分布。

这个过程可以用数学公式来表示：如果X和Y都是伽马分布的随机变量，且它们的形状参数分别为α和β，尺度参数相同，那么X/Y将服从贝塔分布，其形状参数为α和β。

这个数学原理的背后，是伽马分布和贝塔分布之间的一种特殊关系，即它们都是广义指数家族的一部分。这种关系使得我们可以利用伽马分布的性质来研究贝塔分布，反之亦然。

三、伽马分布相除为贝塔的实际应用

伽马分布相除为贝塔的数学原理，在实际应用中有着广泛的应用。例如，在金融领域，我们可以利用这一原理来研究资产的风险敞口比例；在生物学领域，我们可以用它来研究种群的动态变化。

此外，这一原理还可以应用于机器学习和人工智能领域。例如，当我们需要对一个未知的数据分布进行建模时，我们可以先假设它服从某种已知分布，然后通过训练数据来学习这个分布的参数。在这个过程中，伽马分布和贝塔分布都可以作为我们的候选分布。

四、结语

伽马分布相除为贝塔，这个看似简单的数学操作，实际上蕴含了深刻的数学原理和广泛的实际应用。通过对这一问题的探讨，我们可以更好地理解这两种分布之间的关系，以及它们在解决实际问题中的作用。

在未来的研究中，我们期待有更多的学者和实践者关注这一问题，发掘出更多有趣的数学现象和应用。