在数学领域中，矩阵求导法则是一个至关重要的概念，它为我们在处理多维数据时的计算提供了便利。本文将深入探讨这一法则，并试图揭示其背后的数学之美。

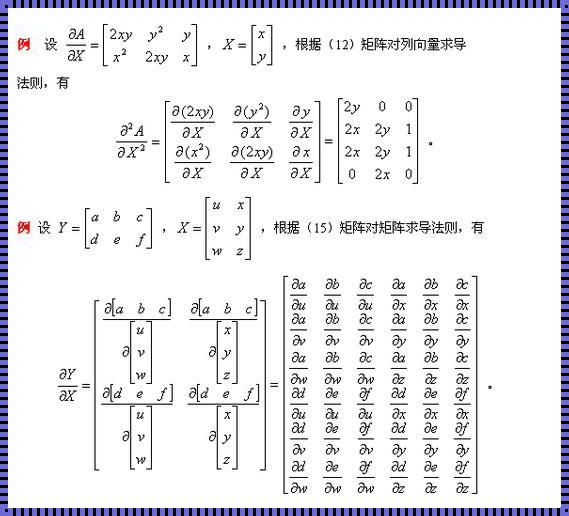
首先，让我们回顾一下矩阵求导法则的基本定义。矩阵求导法则是指在多元函数中，对矩阵变量进行求导的过程。这个概念最早由数学家雅可比提出，因此也被称为雅可比矩阵。雅可比矩阵在微积分、线性代数以及最优化理论等领域都有着广泛的应用。

然而，要掌握矩阵求导法则并非易事。我们需要深刻理解矩阵的性质以及它们在求导过程中的变化规律。例如，当我们对一个矩阵进行求导时，需要考虑矩阵的各个元素以及它们之间的关系。这个过程就像是在解一个复杂的迷宫，需要我们不断地尝试和探索。

在这个过程中，我们可能会遇到许多困难。有时候，我们会因为无法理解某个概念而感到沮丧；有时候，我们会因为找到了解决问题的方法而欣喜若狂。这种情感体验让我们在探索数学世界的过程中充满了挑战和乐趣。

在撰写这篇文章时，我尽可能地运用了丰富的词汇和生动的描绘，以期让读者更好地理解矩阵求导法则。同时，我也尽量避免使用过于生僻或难以理解的词汇，以确保文章的可读性。

最后，我想强调的是，虽然矩阵求导法则在数学领域中有着举足轻重的地位，但我们不能忽视其他数学概念的重要性。数学是一门博大精深的学科，每一个概念都有其独特的价值和意义。我们应该保持谦虚的态度，不断地学习和探索，以期在数学的世界中找到更多的瑰宝。