正四面体作为几何学中的一种基本立体图形，其二级结论的研究对于理解空间几何结构具有重要意义。本文将深入探讨正四面体的二级结论及其影响，以期揭示其在数学理论与实际应用中的价值。

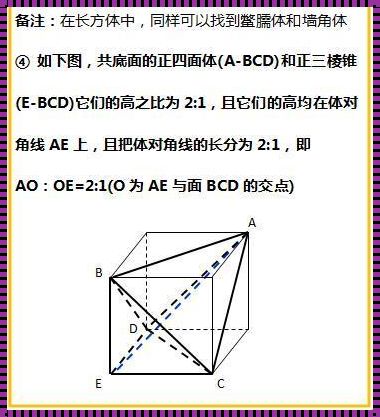
首先，我们要明确什么是正四面体的二级结论。所谓二级结论，是指在研究正四面体的基本性质（如边长、面积、体积等）的基础上，进一步推导出的具有一定普适性的规律或定理。这些结论不仅丰富了正四面体的理论体系，还为解决实际问题提供了有力的工具。

例如，正四面体的二级结论之一是关于其内角和外角的性质。通过研究发现，正四面体的内角和外角之间存在一定的关系，这种关系有助于我们更好地理解正四面体的对称性和稳定性。在实际应用中，这一结论对于设计具有高稳定性的结构具有重要意义。

此外，正四面体的二级结论还包括其边长、面积和体积之间的关系。通过对这些关系的深入研究，我们可以得出一系列具有普遍意义的公式和定理，这些公式和定理在解决空间几何问题时具有很高的实用价值。

然而，正并非孤立存在，它们之间存在着密切的联系。通过对这些结论的综合分析，我们可以发现正四面体的一些深层次规律，这对于推动几何学的发展具有重要意义。

总之，正及其影响是我们研究空间几何结构的重要切入点。通过对这些结论的深入研究，我们可以更好地理解正四面体的性质，为解决实际问题提供有力的理论支持。同时，这也为我们提供了一个全新的视角，去审视和理解几何学的其他领域。