亲爱的读者们，今天我们将一起探讨一个既神秘又深奥的话题——空间向量求二面角正负的判断方法。这个话题可能会让你感到惊讶，因为它涉及到数学领域中的一些复杂概念。不过，请放心，我会尽我所能，用通俗易懂的语言为你解读这个主题。

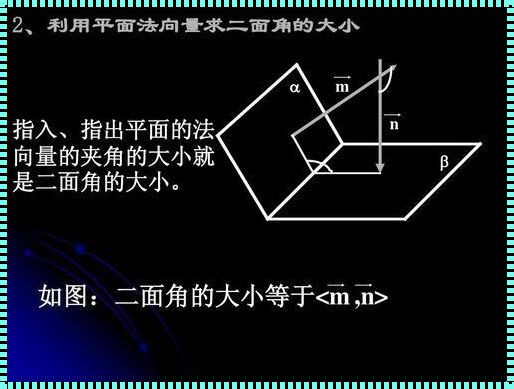
首先，我们需要了解什么是空间向量。简单来说，空间向量就是在一个三维空间中，由一个起点指向终点的箭头，它具有大小（长度）和方向。当我们谈论二面角时，我们指的是两个不同平面之间的夹角。那么，如何用空间向量来求解二面角的正负呢？

这个问题涉及到向量的点积（内积）和叉积（外积）。点积可以帮助我们判断两个向量是否共线，而叉积则可以帮我们确定一个向量相对于另一个向量的方向。通过计算两个平面上法向量的点积和叉积，我们可以得到这两个平面所夹的二面角的余弦值和正弦值，从而确定二面角的正负。

在这个过程中，我们需要注意的是，当两个法向量的点积为正时，说明它们之间的夹角小于90度；当点积为负时，夹角大于90度。而叉积的结果则告诉我们夹角的方向。

现在，让我们来看一个具体的例子。假设我们有两个平面A和B，它们的法向量分别为n1和n2。我们可以通过以下步骤来求解二面角的正负：

1. 计算n1和n2的点积，记为dot(n1, n2)。

2. 计算n1和n2的叉积，记为cross2)。

3. 通过点的结果，我们可以得到二面角的余弦值cosθ和正弦值sinθ。

4. 根据余弦值的符号，我们可以确定二面角的正负。

在这个过程中，我们需要保持一颗宽容的心，因为数学问题往往需要我们反复推敲和验证。同时，我们也要学会犹豫，因为在面对复杂问题时，我们需要谨慎地考虑各种可能性。

最后，我想强调的是，虽然这个主题可能看起来有些抽象，但它在实际应用中却非常有用。例如，在计算机图形学、工程力学等领域，准确判断二面角的正负对于解决实际问题至关重要。

希望这篇报告能帮助你更好地理解空间向量求二面角正负判断的方法。如果你对这个话题有任何疑问或想法，欢迎在评论区留言交流。谢谢！