线性同余法mod计算，一个听起来颇有些神秘的数学领域，其实质却是解决同余方程的巧妙工具。同余方程，一种形如a x ≡ b (mod m)的方程，其中a、b、m是已知整数，x是待求解的整数，一直以来都是数论中的难题。然而，线性同余法mod计算的出现，让这个难题变得不再遥不可及。

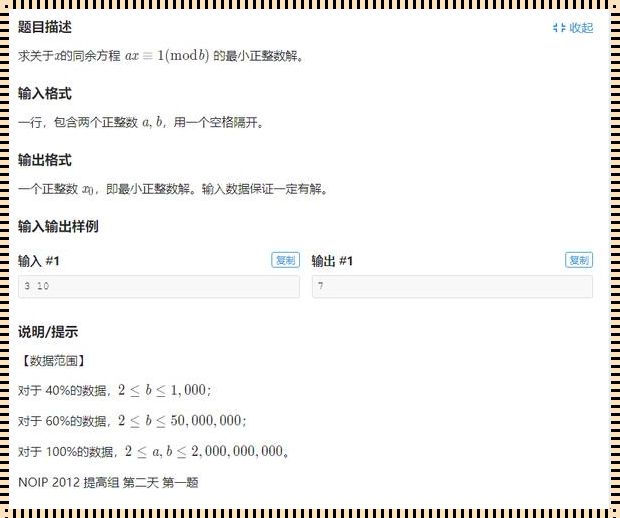
线性同余法mod计算的核心思想，是将同余方程转化为一个关于x的线性方程，然后通过扩展欧几里得算法求解这个线性方程。听起来似乎有些复杂，但其实，线性同余法mod计算的过程就像是一场探险，每一步都充满了未知和挑战。

首先，我们令y ≡ x (mod m)，然后将y代入原同余方程，得到a y ≡ b (mod m)。这一步，就像是我们在迷宫中找到了一条新的路径，将原本复杂的同余方程简化为了一个线性方程。

接下来，我们使用扩展欧几里得算法求解这个线性方程。扩展欧几里得算法，是一种求解线性同余方程组的方法，其基本思想是不断地用较小的模去除较大的模，直至模数为1。这一步，就像是我们在探险过程中，用我们的智慧化解了一个又一个的难题，最终找到了迷宫的出口。

在这个过程中，我们需要注意的是，每次计算过程中，同余方程的系数和常数都需要取模；当模数为1时，计算结果即为方程的解；若计算过程中出现除以0的情况，需要重新计算。这些注意事项，就像是我们在探险过程中需要遵守的规则，只有严格遵守，才能顺利找到迷宫的出口。

总的来说，线性同余法mod计算就像是破解数论谜题的一场探险，虽然过程中充满了未知和挑战，但只要我们掌握了正确的方法，就能轻松破解这个谜题。