在图论的广袤宇宙中，完全图这一概念犹如一颗璀璨的星辰，以其独特的魅力吸引着无数研究者。完全图，一种每对不同顶点间都有一条边的特殊图，其简洁的定义背后隐藏着复杂的数学原理与深刻的理论价值。那么，完全图究竟是否属于简单图呢？让我们一探究竟。

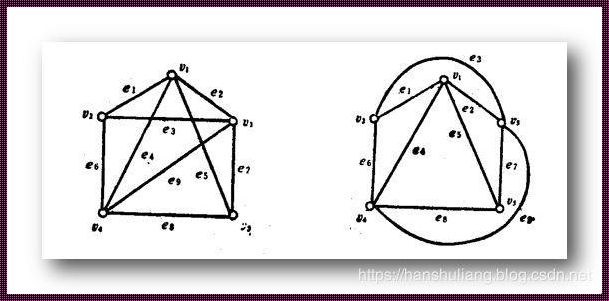
图论作为数学的一个分支，以图为研究对象，探讨其在各个领域的应用。图由顶点和边构成，作为一种数学模型，它在计算机科学、信息科学、经济学等领域发挥着重要作用。完全图，作为图论中的一个基础概念，其特殊性在于任意两个不同的顶点之间都存在一条边。尽管其定义看似简单，但其内在的性质和结构却异常复杂。

关于完全图是否为简单图的问题，答案是肯定的。简单图要求图中的顶点和边数量有限，且不存在重复的边和顶点。完全图恰好满足这些条件，因此可以将其视为一种简单图。然而，正是这种简单性赋予了完全图独特的地位和重要性。

完全图的复杂性表现在多个层面。首先，完全图的顶点数和边数之间的关系具有特殊规律。对于一个包含n个顶点的完全图，其边数为n(n-1)/2，这一数学公式揭示了完全图的一个重要特征。其次，完全图还具有其他独特性质，如所有顶点的度都相等，这在图论中是独一无二的。

完全图的这些特性使其在众多领域得到广泛应用。在计算机科学中，完全图用于模拟网络结构和通信协议；在信息科学中，它有助于分析信息的传播过程；而在经济学则被用于研究市场结构和经济网络综上所述，完全图确实是一种简单图，但其内在的复杂性和独特性使其在图论中占有举足轻重的地位。深入研究完全图不仅有助于揭示图论中的深层次原理，还能为图论的实际应用开辟新途径。完全图的魅力在于其简单与复杂的完美结合，让我们共同探索这一神秘领域的无限可能。