在数学的海洋中，线性空间和向量空间这两个概念常常让人困惑。它们之间究竟有什么联系呢？让我们一探究竟。

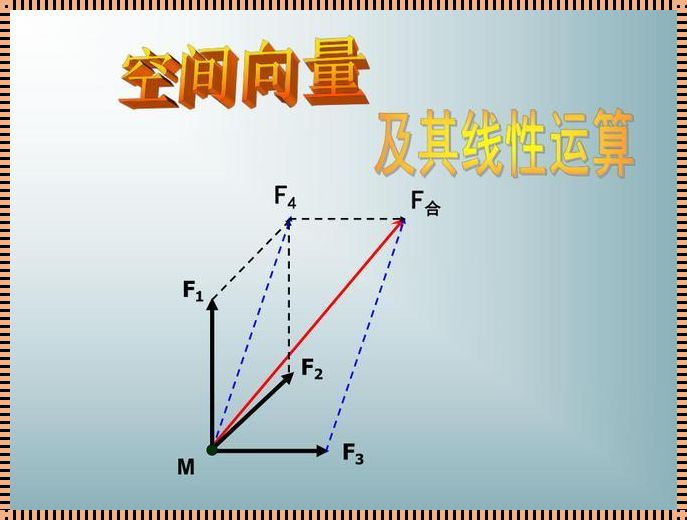
首先，我们来定义这两个概念。线性空间，又称为向量空间，是一种特殊的集合，其中的元素可以进行加法和标量乘法运算，并且这些运算满足一定的公理。然而，当我们提到向量空间时，我们通常指的是一个具体的实例，其中元素不仅包括数值，还包括方向。

现在，回到我们的问题：线性空间一定是向量空间吗？答案是否定的。虽然向量空间是线性空间的一个特例，但线性空间本身并不一定包含方向这一属性。换句话说，线性空间可以是一个更广泛的集合，其中可能包含一些不具有方向的元素。因此，我们不能简单地认为所有的线性空间都是向量空间。

在这个问题上，我们看到了数学的严谨性和逻辑性。每个概念都有其明确的定义，不同概念之间的关系也是清晰明确的。这种严谨的态度对于确保我们在研究数学问题时保持准确性和可靠性至关重要。

在线性空间和向量空间的关系上，我们可以将其比作一个家庭。向量空间是这个家庭中的一个特殊成员，它具有独特的性质和特征。而线性空间则是这个家庭的家长，它包含了向量空间以及其他不满足向量空间定义的元素。这种包含与被包含的关系使它们的关系更加丰富和有趣。

通过深入研究线性空间与向量空间之间的关系，我们可以更好地理解线性代数中的基本概念，为我们的学习和研究奠定坚实的基础。同时，这个问题也提醒我们在研究其他问题时，要保持同样的严谨态度。

总的来说，线性空间和向量空间之间的关系是复杂且有趣的。它们之间的差异和联系为我们提供了一个深入了解数学世界的窗口。在这个过程中，我们不仅要关注概念的定义和性质，还要关注它们之间的关系。只有这样，我们才能更好地理解和运用这些概念，从而在数学的道路上走得更远。