在物理、工程和计算机科学等领域，判断向量方向相同是一个基础数学概念。然而，对于如何准确判断向量方向相同，却存在一些误解和谬论。本文将辟谣常见的错误说法，并介绍三种简单方法来判断向量方向相同。

辟谣：仅靠夹角判断向量方向相同

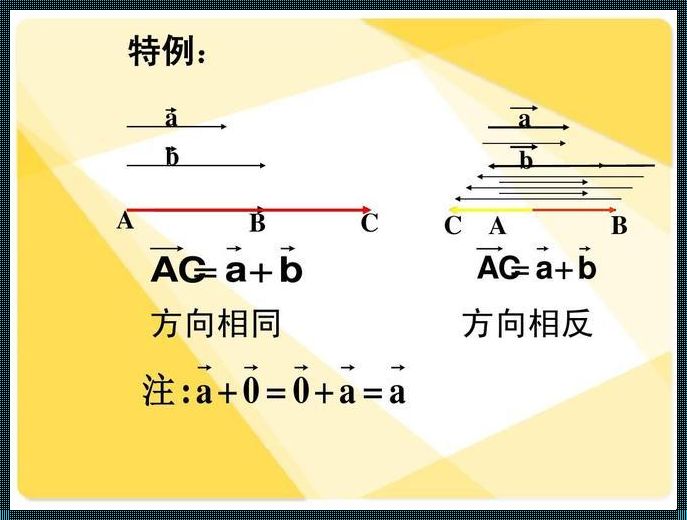
有人误认为，向量方向相同仅靠夹角就可以判断。实际上，这种说法是错误的。夹角大小仅能帮助我们判断向量的相对方向，但它无法确定向量是否相同。例如，两个向量可以有相同的夹角，但它们的方向并不相同。这可以通过一个简单的例子来说明：如果我们把两个向量放在一条直线上，那么它们的夹角为零，但它们的方向显然不同。

方法一：比较向量分量

判断向量方向相同的第一种方法是比较它们的向量分量。如果两个向量在每个分量上都具有相同的值，那么这两个向量方向相同。例如，两个向量(1, 2, 3)和(4, 6, 9)，它们的向量分量分别是(1, 2, 3)和(4, 6, 9)。由于它们的每个分量都相同，因此这两个向量的方向相同。

方法二：使用向量点积

判断向量方向相同的一种更直接的方法是使用向量点积。向量点积是两个向量之间的数量乘积，它可以用来表征两个向量的相对方向。如果两个向量方向相同，那么它们的向量点积为正数。如果两个向量方向相反，那么它们的向量点积为负数。如果两个向量垂直，那么它们的向量点积为零。例如，两个向量(1, 2, 3)和(4, 6, 9)的向量点积为(1)(4) + (2)(6) + (3)(9) = 4 + 12 + 27 = 43，是一个正数，因此这两个向量的方向相同。

方法三：利用叉积判断

当向量方向相同的时候，叉积为0；反之，叉积不为0。利用这一个性质，我们也可以轻松的判断两个向量的方向。例如，两个向量(1, 2, 3)和(4, 6, 9)的叉积为(i)(6-9)+(-j)(9-12)+(k)(2-4)=3i+3j-2k。因此，叉积不等于0，这两个向量方向不同。

总结

综上所述，判断向量方向相同的方法有很多，包括比较向量分量、使用向量点积以及利用叉积判断。这些方法简单易用，可以帮助我们清楚地判断出两个向量的相对方向。在学习数学的过程中，我们需要严谨对待每一个概念，避免误解和谬论，才能更好地理解和掌握数学知识。