自古以来，数学家们便致力于探究复数的世界。其中，复数的模概念更是引人入胜。那么，abs 函数能否求解复数的模呢？答案自然是肯定的。

一、abs 函数与复数模的关联

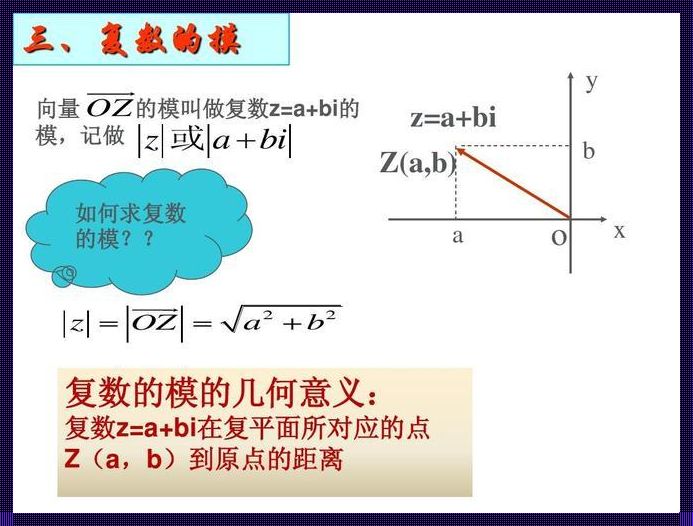
我们知道，复数可以表示为 a+bi 的形式，其中 a 为实部，b 为虚部。而复数的模，即为其与原点之间的距离。那么，如何用 abs 函数来求解复数的模呢？

二、abs 函数在复数模求解中的应用

1. 当 b=0 时，复数为实数，此时 abs 函数求解的正是复数的模。

2. 当 b≠0 时，复数为虚数或复数，我们可以通过以下步骤求解其模：

首先，计算复数的共轭复数，即 a-bi。

接着，求解两复数的乘积，得到 (a+bi) * (a-bi) = a^2 + b^2。

最后，求解上式的绝对值，即|a^2 + b^2|，得到复数的模。

三、总结

综上所述，abs 函数确实可以求解复数的模。无论是实数、虚数还是复数，只需将其转换为相应的形式，运用 abs 函数即可轻松求得模值。这也体现了数学的神奇与美妙，让我们不禁为之赞叹。

然而，复数的世界远不止于此。我们还可以进一步探讨复数的其他性质，如共轭复数、复数的乘法与除法等。相信通过不断探索，我们会对复数有更深入的了解。

复数之魅，源于其丰富的内涵。让我们携手，继续探索这神奇的世界，挖掘其背后的规律与真理。