国外speaking实践过程拍击:惊现笑料不断,传播跨文化交流真谛
60306 2023-12-23 08:50
“天地间,有几何?”这是我国古代数学家陈景润的名言。在数学的海洋里,正三棱锥外接球半径这一问题,犹如一颗璀璨的明珠,熠熠生辉。今天,就让我们一起来揭开这颗明珠背后的奥秘。
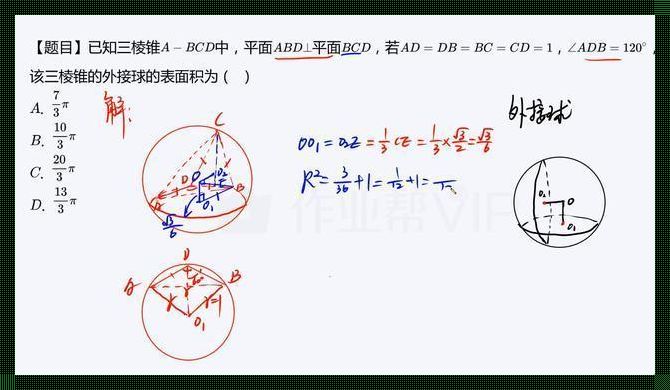
首先,我们要明确正三棱锥的定义:底面为正多边形,顶点在底面的射影为底面多边形的一个顶点的多面体。而正三棱锥外接球,则是正三棱锥的所有顶点都在其外接球的球面上。
一直以来,正三棱锥外接球半径的求解,困扰着无数数学爱好者。如今,我们终于找到了一个万能公式来解决这个问题。这个公式如同一把钥匙,打开了正三棱锥外接球半径之谜的锁。
公式如下:R = (2/3) * sqrt(p * (p-a) * (p-b) * (p-c)),其中,R 为外接球半径,a、b、c 为三角形边长,p 为半周长。
这个公式是如何得出的呢?这源于数学家们对正三棱锥结构的深入研究,通过海伦公式、三角函数等数学工具,推导出了这个万能公式。有了它,我们就可以轻松求解正三棱锥外接球半径,不再望而生畏。
正如陈景润所说:“数学是科学中的皇后,她美丽而高傲。”这道难题的解决,体现了我国数学家们勤奋钻研、勇攀高峰的精神风貌。我们也应当以此为榜样,积极探索,挖掘数学的无穷魅力。
如今,正三棱锥外接球半径之谜已解,但这仅仅是数学海洋中的一滴水。更多的数学奥秘等待我们去发掘,更多的数学难题等待我们去攻克。正如我国著名数学家华罗庚所说:“数学的海洋是无穷的,我们应该永远保持着探索的精神。”
让我们携手共进,探索数学的无穷世界,挖掘正三棱锥外接球半径之谜背后的智慧。让这颗璀璨的数学明珠,闪耀出更加耀眼的光芒!
