自古以来，几何学便是数学领域中一颗璀璨的明珠，而正三棱锥则是几何学中一个充满魅力的研究对象。我们或许曾在数学课上听说过它，也可能在某个角落里瞥见过它的身影，但你是否真正了解过它，又是否知道如何求出它的高呢？

首先，让我们来揭开正三棱锥的神秘面纱。正三棱锥，顾名思义，是一个底面为正三角形的三维几何体。它有四个顶点，其中三个位于底面上，另一个则位于底面的正上方。它的侧面是三个全等的等腰三角形，底面与侧面相交，形成三个等边三角形。

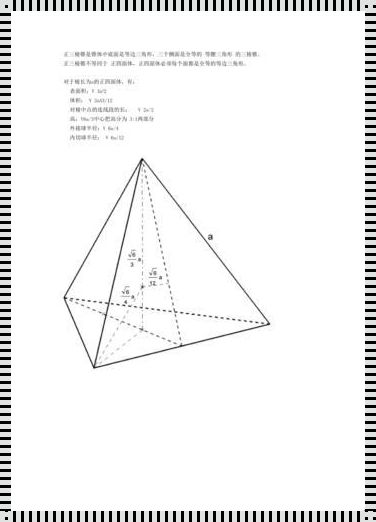
那么，如何求出正三棱锥的高呢？这里，我们可以运用几何知识和数学公式。设正三棱锥的高为h，底面边长为a，我们可以通过以下步骤求出它的高。

首先，我们画出正三棱锥的图形，并将其高h、底面边长a和侧面高l标出来。然后，我们可以通过观察和推理，发现正三棱锥的高h与底面边长a和侧面高l之间存在一定的关系。

通过观察，我们可以发现，正三棱锥的高h实际上是侧面高l与底面边长a的垂直距离。因此，我们可以得出结论：正三棱锥的高h等于侧面高l与底面边长a的垂直距离。

那么，如何求出侧面高l呢？这里，我们可以运用勾股定理。在正三棱锥中，侧面高l与底面边长a和侧面斜边b之间存在一定的关系。具体来说，侧面高l的平方等于侧面斜边b的平方减去底面边长a的平方。

因此，我们可以得出公式：l = √(b² - a²)。然后，我们将这个公式代入到求正三棱锥高的公式中，即可得出正三棱锥的高h。

总的来说，求正三棱锥的高需要运用几何知识和数学公式，通过观察和推理，我们可以发现正三棱锥的高与底面边长和侧面高之间存在一定的关系。通过勾股定理，我们可以求出侧面高，进而求出正三棱锥的高。

在这个过程中，我们不仅可以感受到数学的严谨和美感，还可以锻炼我们的逻辑思维和推理能力。正三棱锥的高怎么求，这个问题看似简单，但却蕴含着丰富的数学知识和几何美学。通过这个问题，我们可以惊现数学之美，感受到数学的魅力和力量。