众所周知，内插法计算例子是数学计算中的一个重要方法，其基本思想是根据已知数据在某个区间内推算出未知数据的近似值。然而，内插法不仅仅是一个简单的数学工具，更是一种思维方式，一种解决问题的策略，其应用范围广泛，涉及到生活中的方方面面。本文将围绕内插法计算例子，进行一次全方位的深入探究与运用。

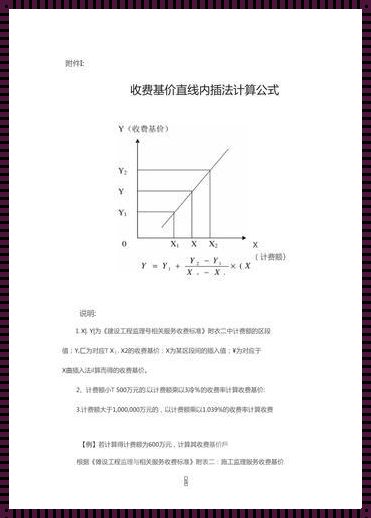
首先，我们要明确内插法的基本概念。内插法是指在已知两个或多个数据点的情况下，通过构建一个函数模型，在这些点之间的某个位置推算出未知数据的近似值。这个方法的关键在于找到合适的函数模型和合适的插值点。常见的内插法包括线性插值、二次插值、样条插值等。

内插法在科学研究中的应用尤为广泛。例如，在物理实验中，我们常常需要测量某个物理量的值，但由于实验条件的限制，我们可能无法直接测量到这个值。这时候，我们就可以通过内插法，根据已知的物理量值，推算出未知的物理量值。同样，在化学实验中，我们也可以通过内插法，根据已知的浓度值，推算出未知的浓度值。

内插法在工程技术中的应用也非常广泛。例如，在工程设计中，我们常常需要根据已知的工程数据，推算出未知的工程数据。这时候，我们就可以通过内插法，根据已知的工程数据，推算出未知的工程数据。又如，在计算机图形学中，我们常常需要根据已知的像素值，推算出未知的像素值。这时候，我们就可以通过内插法，根据已知的像素值，推算出未知的像素值。

内插法在经济学中的应用也非常广泛。例如，在经济学研究中，我们常常需要根据已知的经济发展数据，推算出未知的经济发展数据。这时候，我们就可以通过内插法，根据已知的经济发展数据，推算出未知的经济发展数据。又如，在金融分析中，我们常常需要根据已知的金融数据，推算出未知的金融数据。这时候，我们就可以通过内插法，根据已知的金融数据，推算出未知的金融数据。

通过上述的例子，我们可以看到，内插法计算例子不仅仅是一个简单的数学工具，更是一种思维方式，一种解决问题的策略。无论是在科学研究中，还是在工程技术中，还是在经济学中，内插法都可以帮助我们解决很多实际问题。因此，我们应该深入理解和掌握内插法，以便在解决实际问题时，能够更好地运用它。