在我国传统的几何学中，正三棱柱是一种极具美感的几何体，而它的内外切球半径更是几何学中的瑰宝。对于许多人来说，这可能是一个陌生的概念，但它却蕴含着丰富的数学内涵和实际应用价值。今天，就让我们一同踏上这场探索正三棱柱内外切球半径的奇妙之旅。

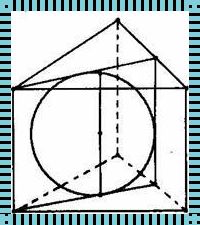
首先，我们需要明确正三棱柱的定义。正三棱柱是一种底面为等边三角形，侧面为矩形的三棱柱。在正三棱柱中，底面的边长与侧面的高度相等，侧面的宽度与底面的边长垂直。正三棱柱的内外切球半径是指球在正三棱柱内部和外部的切点与球心的距离。

在探索正三棱柱内外切球半径的过程中，我们不得不提的是欧拉公式。欧拉公式是几何学中一个重要的公式，它揭示了正多面体和球之间的关系。欧拉公式表达为：V - E + F = 2，其中V代表多面体的顶点数，E代表多面体的边数，F代表多面面的面数。对于正三棱柱，我们可以通过欧拉公式计算出其内外切球半径。

然而，仅仅了解公式是远远不够的。我们还需要深入理解正三棱柱内外切球半径的几何意义。正三棱柱的内外切球半径实际上揭示了正三棱柱与球之间的紧密联系。通过研究正三棱柱的内外切球半径，我们可以更好地理解几何体的性质，从而为实际应用提供理论依据。

在现实生活中，正三棱柱内外切球半径的应用十分广泛。例如，在建筑设计中，我们可以通过计算正三棱柱的内外切球半径来确定建筑物的结构稳定性。在制造业中，正三棱柱内外切球半径的计算可以帮助我们优化产品的设计，提高生产效率。此外，在地理学、气象学、光学等领域，正三棱柱内外切球半径也有着广泛的应用。

当然，探索正三棱柱的内外切球半径并非易事，它需要我们具备扎实的几何学基础和丰富的想象力。然而，正是这种挑战性使得正三棱柱内外切球半径的探索成为一场充满奇遇的旅程。在这场旅程中，我们不仅可以领略到几何学的优美与和谐，还可以锻炼我们的思维能力，提高我们的解题技巧。

总之，正三棱柱的内外切球半径是几何学中一个极具魅力的课题。通过探索正三棱柱的内外切球半径，我们可以深入了解几何体的性质，为实际应用提供理论依据。同时，这场探索之旅也将成为我们丰富想象力、提高思维能力的绝佳机会。让我们携手踏上这场几何世界的奇妙之旅，共同探索正三棱柱内外切球半径的无穷奥秘。