数学，一门充满神秘与奇妙的学科，总是在不经意间展现出它的独特魅力。在这个充满数字与符号的世界里，有一个概念格外引人入胜，那就是“逆元”。那么，什么是逆元呢？它又有怎样的求法呢？接下来，让我们一同踏上这场探索之旅。

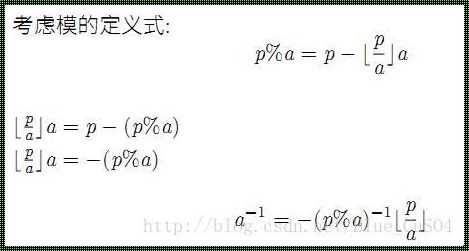
首先，我们需要了解逆元的定义。在数学中，逆元是指在一个数学结构中，与某个元素相对应的另一个元素，它们之间的运算结果为单位元。例如，在群论中，一个元素的逆元就是与它相乘后得到单位元的元素。那么，如何求一个元素的逆元呢？

求逆元的方法有很多，这里我们介绍几种常用的方法。首先是伴随矩阵法。对于一个可逆矩阵，它的逆矩阵就是它的伴随矩阵除以它的行列式。这种方法适用于各种类型的矩阵，包括对称矩阵、反对称矩阵等。其次，是利用行列式和矩阵的逆的性质。对于二阶矩阵，我们可以通过计算它的行列式和伴随矩阵来求逆。对于高阶矩阵，我们可以通过将矩阵转化为上三角矩阵，然后利用上三角矩阵的逆的性质来求逆。

除了这些传统的求法，还有一些更为高效的算法，如高斯-约当消元法、LU分解法等。这些方法在实际应用中有着广泛的应用，如线性方程组的求解、最小二乘法的实现等。

然而，求逆元并非总是那么顺利。在某些情况下，元素可能没有逆元，或者求逆过程异常复杂。这时，我们需要寻找其他的解决方案，如利用近似算法、迭代法等。这些方法虽然不能给出精确的逆元，但可以给出一个足够接近的解，满足实际应用的需求。

总的来说，逆元的求法是数学中一个充满挑战和奇妙的领域。它不仅需要我们掌握扎实的数学知识，还需要我们具备灵活的思维和创新的意识。正如著名数学家华罗庚所说：“数学是自然的皇后，是科学的皇后。”在这片广阔的数学天地里，我们每个人都是一位探险家，不断寻求新的发现和突破。