在概率论和统计学中，分布是描述随机变量取值可能性的一种方式。其中，三角分布和均匀分布是最常见的两种连续概率分布。它们在实际应用中有着广泛的应用，比如在质量控制、经济预测等领域。

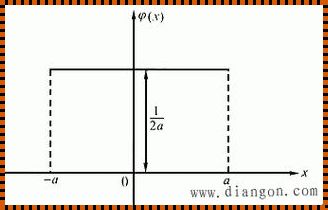
三角分布，顾名思义，其概率密度函数的图形呈三角形。它通常用来描述那些在某个特定区间内递减的随机变量，比如人的身高、物体的重量等。而均匀分布，则是指随机变量在某个区间内取任意值的概率相等。它常用来描述那些没有明显趋势的随机变量，比如掷骰子的结果、彩票中奖号码等。

那么，三角分布和均匀分布之间有什么关系呢？我们可以从以下两个方面来看：

首先，从数学角度来说，三角分布可以看作是均匀分布的一种特例。当均匀分布的区间长度趋近于零时，其概率密度函数的峰值会逐渐变得更加尖锐，最终形成一个三角形。反之，当三角分布的区间长度趋近于无穷大时，其概率密度函数会逐渐变得平缓，最终变成一个常数。

其次，从实际应用角度来说，三角分布和均匀分布可以看作是人们对随机变量认识的不同阶段。在初期，人们可能认为某个随机变量在某个区间内取任意值的概率是相等的，从而选择使用均匀分布来描述。然而，随着对随机变量认识的深入，人们可能会发现这个随机变量并非完全随机，而是在某个特定区间内有一定的递减趋势，此时就可以选择使用三角分布来描述。

然而，尽管三角分布和均匀分布有着紧密的联系，它们在实际应用中也有着显著的区别。三角分布需要我们了解随机变量的具体递减趋势，而均匀分布则不需要。这就导致了在实际应用中，我们需要根据具体情况来选择合适的分布类型。

总之，三角分布和均匀分布关系密切，它们在概率论和统计学中都有着重要的地位。通过深入理解它们之间的关系，我们可以更好地选择合适的概率分布来描述实际问题，从而为解决实际问题提供有力的理论支持。