有向图是图论中的一个重要概念，它是由顶点和有向边组成的。在研究有向图时，一个关键的问题就是判断有向图是否存在回路。回路是指图中有向边形成的闭合路径，即从一个顶点出发，经过若干个顶点后回到出发点的路径。

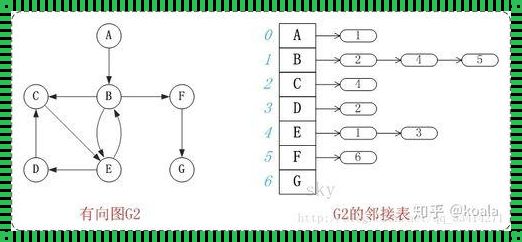
要判断一个有向图是否存在回路，可以采用多种方法。其中一种常用的方法是基于深度优先搜索（DFS）的算法。深度优先搜索算法是一种用于遍历或搜索树或图的算法，它沿着一个分支深入到不能再深入为止，然后回溯到上一个分叉点继续搜索。在执行深度优先搜索的过程中，如果发现从一个顶点出发的所有路径都已经被探索过，那么就意味着存在回路。

另一种方法是基于拓扑排序的算法。拓扑排序是对有向无环图（DAG）进行排序的算法，它将图中的顶点按照一定的顺序进行排序，使得对于任意的有向边(u,v)，u都排在v的前面。如果一个有向图可以进行拓扑排序，那么它就不存在回路。然而，如果无法进行拓扑排序，那么说明图中存在回路。

在实际应用中，判断有向图是否存在回路是非常重要的。例如，在计算机网络中，有向图可以用来表示网络中的节点和边，判断图中是否存在回路可以帮助我们检测网络中的环路，从而避免数据包的无限循环。在编译原理中，有向图可以用来表示源代码的控制流，判断图中是否存在回路可以帮助我们检测源代码中是否存在死循环。

总之，判断有向图是否存在回路是一个关键的问题，它可以通过深度优先搜索算法和拓扑排序算法等方法来解决。这些方法在实际应用中起着重要的作用，帮助我们检测和避免图中存在的环路问题。