马尔科夫状态转移概率矩阵，这个听起来有些晦涩的名字，实际上是概率论中一个非常有用的工具。它以一种简洁明了的方式，描述了一个系统在不同状态之间的转移概率。这种矩阵在许多领域都有广泛的应用，比如物理学、经济学、生物学等。

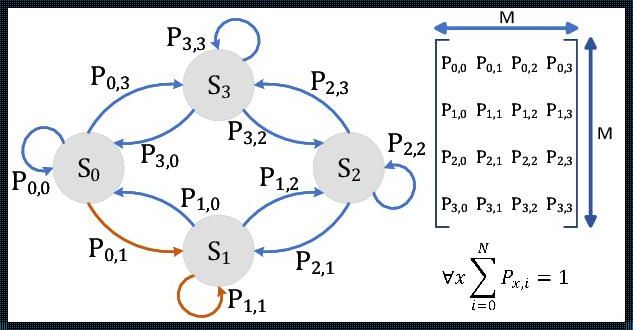
当我们谈论马尔科夫状态转移概率矩阵时，我们实际上是在讨论一个系统的动态行为。这个矩阵告诉我们，在任意时刻，系统处于每个状态的概率是多少，以及这些概率如何随时间变化。这种信息对于理解系统的本质行为和预测其未来状态至关重要。

例如，假设我们正在研究一个简单的物理系统，该系统可以在两种状态之间切换：状态A和状态B。马尔科夫状态转移概率矩阵将告诉我们，在任意时刻，系统处于状态A或状态B的概率。这不仅有助于我们了解系统的当前状态，还可以预测其未来的行为。

马尔科夫状态转移概率矩阵的实际应用非常广泛。在经济学中，它可以帮助我们分析市场的动态变化，预测股票价格的未来走势。在生物学中，它可以帮助我们理解生物种群的动态行为，预测其未来的分布情况。在物理学中，它可以帮助我们分析粒子的行为，预测其在不同状态之间的转移概率。

然而，尽管马尔科夫状态转移概率矩阵在实际应用中非常有效，但它也存在一些局限性。首先，它假设系统的未来状态仅取决于当前状态，而与过去的状态无关。这在许多实际情况下可能并不成立。其次，它假设系统在不同状态之间的转移概率是恒定的。然而，在现实世界中，这些概率可能会随时间变化。

尽管如此，马尔科夫状态转移概率矩阵仍然是一个非常有用的工具。通过深入了解其原理和应用，我们可以更好地理解和预测系统的动态行为。这不仅有助于我们解决实际问题，还可以为我们提供更深入的洞察，帮助我们更好地理解世界。

在这个充满不确定性的世界中，马尔科夫状态转移概率矩阵为我们提供了一种方法，让我们能够从概率的角度看待世界。它教会我们如何从当前的状态推断未来的可能性，以及如何处理和分析复杂系统的动态行为。通过掌握这个工具，我们可以更好地应对未来的挑战，做出更明智的决策。