正四棱锥是一种特殊的几何体，它的底面是一个正方形，四个侧面都是等腰三角形，顶点在底面的正中央。这种几何体在生活中广泛存在，例如我们在建筑、艺术、科学等领域都能找到它的身影。而正四棱锥外接球体积公式，更是几何学中一个重要的公式，它可以帮助我们更好地理解和计算正四棱锥的性质。

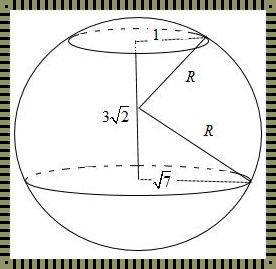
首先，让我们来探讨一下正四棱锥外接球体积公式的推导过程。假设正四棱锥的底面边长为a，高为h，那么它的外接球的半径R可以通过以下公式计算得出：

R = (a^2 + h^2)/4

然后，我们可以通过外接球的半径R来计算正四棱锥的体积V。正四棱锥的体积公式为：

V = (1/3)πR^3

将外接球的半径R代入正四棱锥的体积公式，我们可以得到：

V = (1/3)π((a^2 + h^2)/4)^3

这就是正四棱锥外接球体积公式的推导过程。

然而，对于这个公式，我们应该如何理解和运用呢？首先，我们可以通过这个公式来计算正四棱锥的体积。如果我们知道正四棱锥的底面边长和高，我们就可以通过这个公式来计算它的体积。这对于我们设计和建造建筑物、制作艺术作品等都是非常有益的。

其次，我们可以通过这个公式来研究正四棱锥的性质。例如，我们可以通过改变底面边长和高，来观察正四棱锥外接球体积的变化。这可以帮助我们更好地理解正四棱锥的性质和特点。

最后，我想说的是，正四棱锥外接球体积公式不仅仅是一个几何学中的公式，它更是一种思考和解决问题的方法。通过理解和运用这个公式，我们可以更好地理解和计算正四棱锥的性质，也可以更好地解决与正四棱锥相关的问题。

总的来说，正四棱锥外接球体积公式是一个非常重要的几何学公式，它不仅可以帮助我们计算正四棱锥的体积，还可以帮助我们研究和理解正四棱锥的性质。通过深入探讨和理解这个公式，我们可以更好地运用它，也可以更好地解决与正四棱锥相关的问题。