矩阵求值，对于数学领域来说，是一项基础且重要的工作。当我们遇到一个3x3矩阵时，求值的过程不仅是对矩阵理论知识的一种检验，也是对问题解决能力的一种挑战。

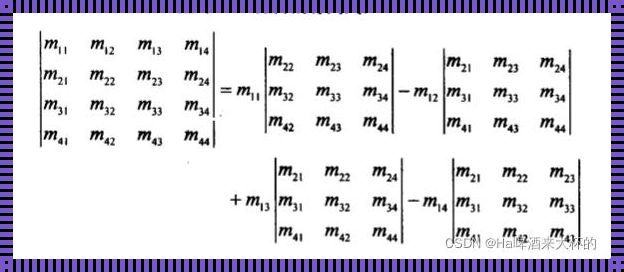
首先，我们需要明确矩阵的概念。矩阵是一个由数字（或函数）排列成的矩形数组。对于一个3x3矩阵，它由3行3列共9个数字组成。例如：

[

a & b & c \ d & e & f \ g & h & i \

]

其中，(a, b, c, d, e, f, g, h, i) 都是实数或复数。

矩阵的求值，通常涉及以下几个步骤：

1. 理解矩阵元素：首先要清楚矩阵中每一个元素的物理意义和数学含义，它们可能代表不同的物理量或者数学运算的结果。

2. 应用矩阵运算法则：包括矩阵的加法、减法、数乘以及矩阵与矩阵的乘法等。对于3x3矩阵，我们可以通过以下方式进行运算：

• 矩阵加法：对应位置上的元素相加。
• 矩阵减法：对应位置上的元素相减。
• 数乘：矩阵每一个元素乘以一个实数。
• 矩阵乘法：遵循“行列式相乘，行数乘以列数”的原则。

1. 求解矩阵方程：当矩阵与特定的向量相结合时，我们可能需要解矩阵方程。例如，求解 (Ax = b)，其中 (A) 是一个3x3矩阵，(x) 是一个3维向量，(b) 是一个已知的向量。

2. 使用矩阵分解：对于某些矩阵，我们可以将其分解为更简单的形式，如对角矩阵、上三角矩阵或下三角矩阵。这有助于简化计算过程。

3. 应用数学软件：在实际操作中，我们经常使用数学软件（如MATLAB、NumPy等）来帮助求解矩阵值，特别是当矩阵较大或者运算较为复杂时。

举个例子，假设我们有以下矩阵：

[

2 & -1 & 3 \ 0 & 4 & -2 \ 1 & 0 & 1 \

]

我们想要求它的值，那么：

• 我们可以简单地将每个元素相加，得到矩阵的和。
• 我们也可以进行矩阵乘法，比如将它与另一个3x3矩阵相乘，或者与一个3维向量相乘。

对于矩阵的求值，我们不仅要在理论上掌握，更要在实践中不断尝试和应用，通过不断的练习，深化对矩阵概念的理解，提高解决实际问题的能力。

在探索矩阵的世界中，每一步都充满了挑战与乐趣。正如一位数学家所说：“矩阵不仅仅是数字的排列，它是一种看待世界的新方法。”让我们一起享受这个探索的过程吧！