在几何学的世界里，四棱锥是一个常见的多面体，它由一个四边形的底面和四个三角形侧面组成，顶点指向底面的中心。对于这样一个看似简单的几何形状，你是否曾经想过，它是否具有内切球呢？

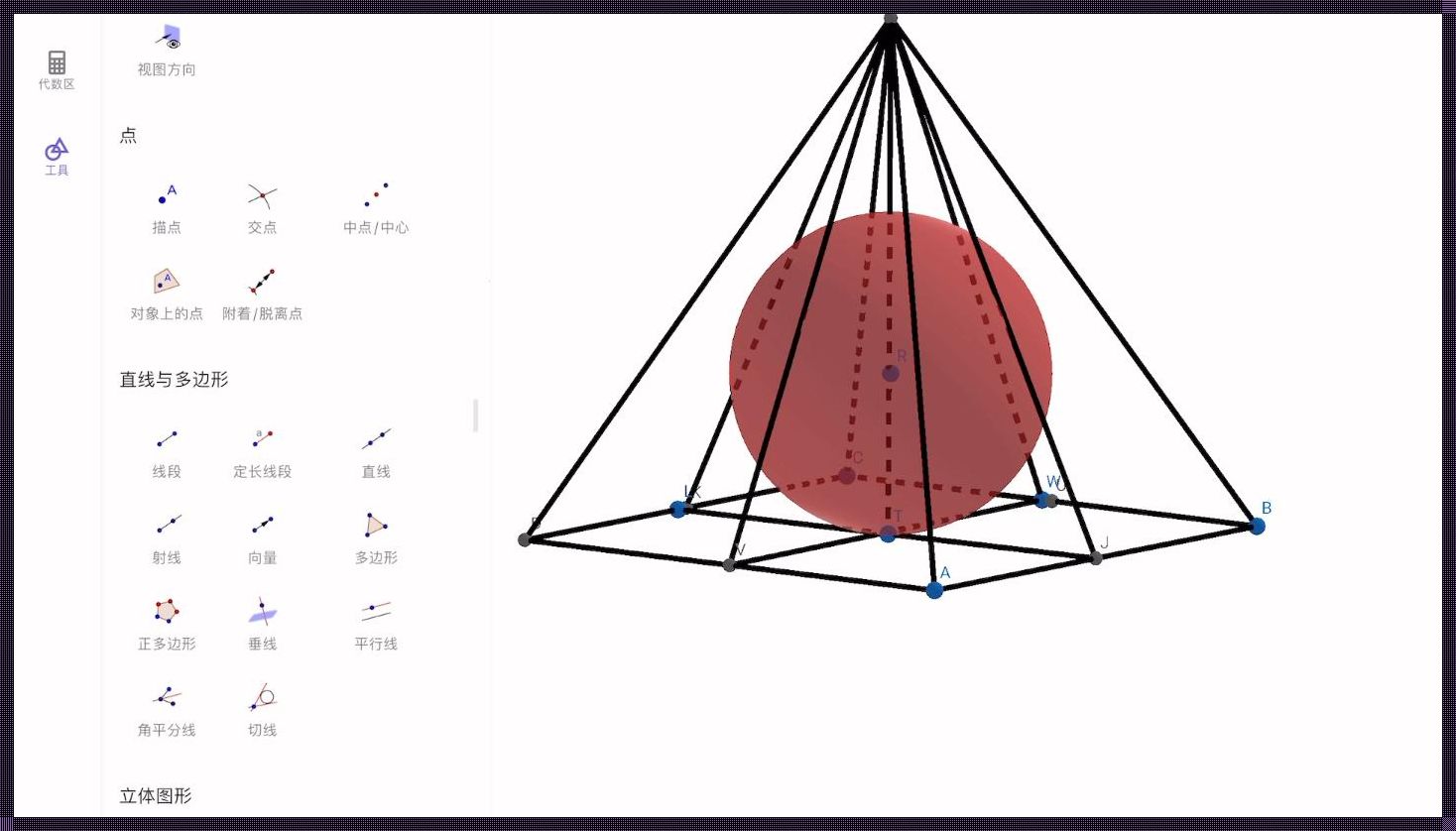
所谓内切球，是指一个球体，它的所有切面都与多面体的面相切。在这个定义下，我们来探讨一下四棱锥是否具有内切球。

首先，我们来看正四棱锥，即底面为正四边形的四棱锥。对于这种四棱锥，我们可以通过构造一个内切球来验证它是否存在。我们可以将四棱锥的四个顶点与底面的中心相连，这样就构成了一个正四面体。而正四面体的内切球同时也是正四棱锥的内切球。由于正四面体的内切球是存在的，因此正四棱锥也具有内切球。

然而，对于一般的四棱锥，情况就有所不同了。一般的四棱锥底面不一定是正四边形，侧面的形状也不一定是三角形。在这种情况下，我们无法直接构造出一个内切球。但是，我们可以通过数学推导来判断是否存在内切球。

假设四棱锥的底面为 (ABCD)，顶点为 (P)，内切球的半径为 (r)。我们可以通过求解四棱锥的体积和表面积，建立 (r) 与四棱锥的边长和高的关系。如果这个关系是存在的，并且对于所有的四棱锥都成立，那么我们可以得出结论：四棱锥都具有内切球。

在探索这个问题的过程中，我们不仅加深了对几何形状的理解，也锻炼了我们的数学推导能力。而这一切，都源于我们对知识的渴望和对未知领域的好奇心。正如古人所说：“学而时习之，不亦说乎？”在探索几何学的奥秘中，我们不断地学习、思考，从而获得了快乐和满足。

最后，让我们以一句名言作为结尾：“好奇心是学习的源泉，满足好奇心是学习的动力。”让我们带着好奇心，继续探索未知领域，追求知识的巅峰！