引言

图论，作为计算机科学和数学领域的重要分支，研究的是图的性质和图上的算法。在诸多图论问题中，kn问题一直备受关注。本文将探讨kn问题的相关概念及回应，并结合实际案例进行分析。

一、kn问题的概念与特点

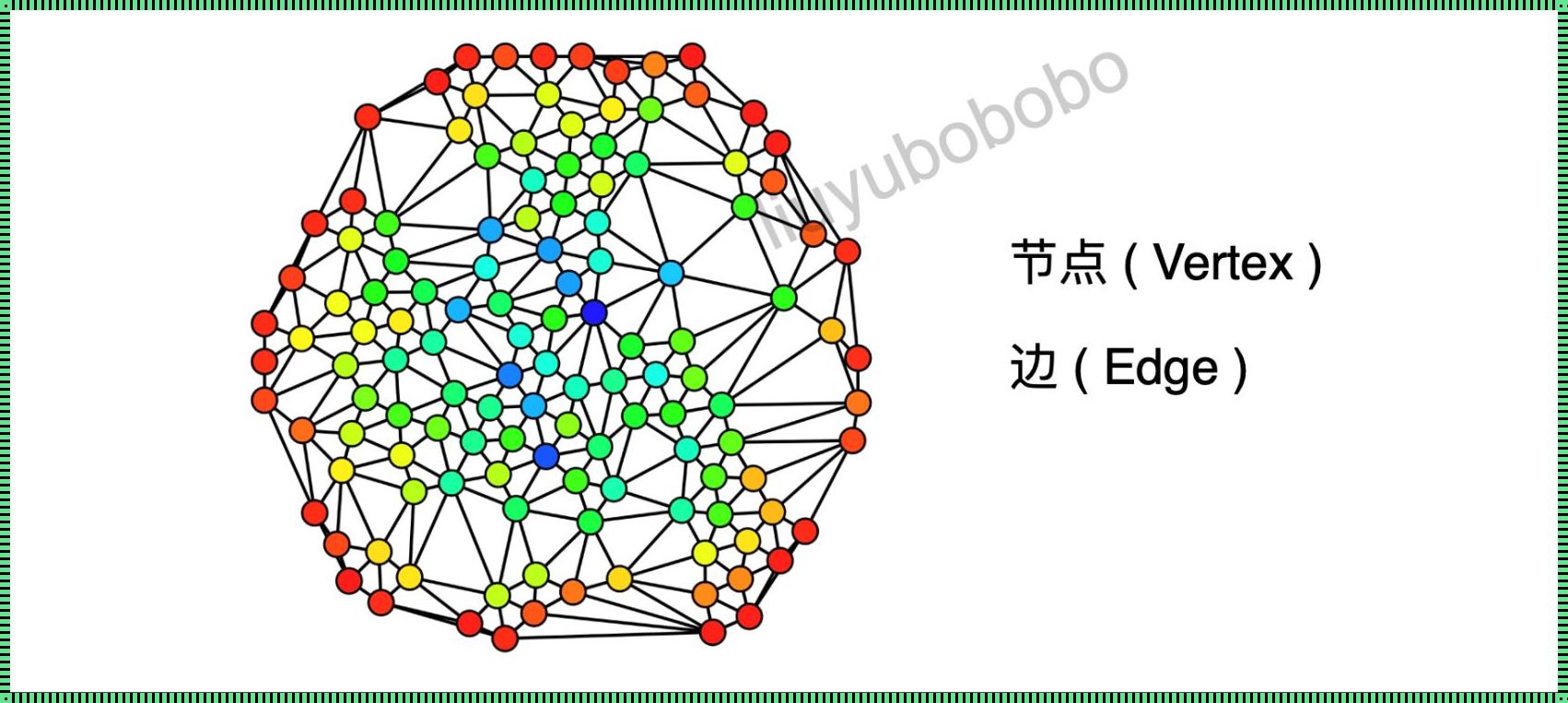
1. kn问题的定义

kn问题，又称结点着色问题，是图论中的一个经典问题。给定一个无向图G=(V,E)，要求给图中的每个结点涂上颜色，使得相邻结点颜色不同，且涂色数量最小。

2. kn问题的特点

（1）最优解的唯一性：对于有解的图G，kn问题的最优解是唯一的。

（2）状态转移方程：用动态规划求解kn问题时，状态转移方程为dp[i][c] = min{dp[j][c'] + 1}，其中c'为与i相邻的结点着色后的颜色。

（3）最长链定理：图G存在最长链，其长度不超过n-1，其中n为图G的结点数。

二、kn问题的回应

1. 回应的定义

回应，又称回帖，是在网络社区中针对某个主题发表的言论。在本篇文章中，我们将针对kn问题在不同场景下的应用，选取具有代表性的回应进行分析。

2. 回应的分类

（1）基于计算法的回应：针对kn问题，研究者们提出了许多高效的算法，如动态规划、贪心算法等。这些算法在实际应用中取得了良好的效果，得到了广泛的回应。

（2）基于问题拓展的回应：在kn问题基础上，研究者们提出了许多拓展问题，如带权kn问题、多色kn问题等。这些拓展问题在一定程度上丰富了kn问题的理论体系，引发了诸多回应。

（3）基于实际应用的回应：kn问题在实际应用中具有重要意义，如在电路设计、地图着色等领域均有广泛应用。针对这些应用场景，人们提出了相应的解决方案，并引发了热烈的回应。

三、kn问题的案例分析

1. 电路设计中的应用

在电路设计中，kn问题可用于优化电路板的布局。通过求解kn问题，可以为电路元件分配最优的颜色，从而使得电路板的空间利用率最高。

2. 地图着色中的应用

在地图着色问题中，kn问题可用于为国家或地区的边界线分配颜色。通过求解kn问题，可以最小化相邻国家或地区颜色的差异，从而使得地图更加美观和谐。

四、结论

本文通过对kn问题的探讨，深入分析了其概念、特点以及在不同场景下的回应。作为图论中的经典问题，kn问题在理论研究和实际应用中都具有重要意义。未来，随着图论的不断发展，相信kn问题将继续成为研究的热点，为我们的生活带来更多便捷与惊喜。