主成分分析法（PCA）是一种常用的数据降维方法，其目的是通过保留数据集中的主要特征分量来减少数据的维数，从而简化模型的复杂度并提高计算效率。在进行主成分分析时，如何选取主成分是一个关键的问题。

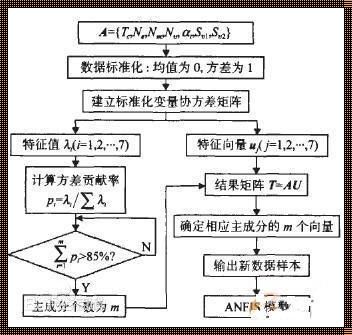
一般来说，选取主成分的方法有以下几种：

1. 按特征值大小排序：首先计算数据集的协方差矩阵，然后求解其特征值和特征向量。将特征值从大到小排序，并选取前k个最大的特征值对应的特征向量作为主成分。

2. 累积解释率：计算每个主成分的解释率（即该主成分所解释的方差的比例），然后将前k个主成分的累积解释率与事先设定的阈值进行比较。当累积解释率超过阈值时，停止添加新的主成分。

3. 留一法（LOO）：在每次迭代中，将一个样本作为测试集，其余样本作为训练集，然后使用训练集计算主成分。通过比较不同主成分的模型性能，选取最佳的主成分。

4. 基于模型的选择：根据实际应用中的模型需求，结合模型的复杂度和性能，选取合适的主成分。例如，在分类任务中，可能需要更多的主成分以获取更多的特征信息；而在回归任务中，过多的主成分可能会导致过拟合。

选取主成分时，需要权衡模型的解释能力和预测能力。过多的主成分可能会导致模型过拟合，而较少的主成分可能会丢失重要的特征信息。因此，在实际应用中，需要根据具体问题和数据集的特点，选择合适的方法和阈值来确定主成分的数量。

主成分分析法在许多领域都有广泛的应用，如图像处理、机器学习、数据挖掘等。通过选取合适的主成分，可以有效地降低数据的维数，简化模型的复杂度，提高计算效率，并在一定程度上提高模型的性能。然而，主成分分析法也有其局限性，如对异常值敏感、无法处理非线性关系等。因此，在使用主成分分析法时，需要结合具体问题和数据集的特点，合理地运用和调整主成分的数量。