t检验是统计学中的一种常用假设检验方法，主要用于比较两个样本均值是否存在显著差异。在进行t检验时，我们通常会得到一个p值，这个p值对于判断检验结果是否显著具有重要意义。那么，p值到底是如何计算出来的呢？

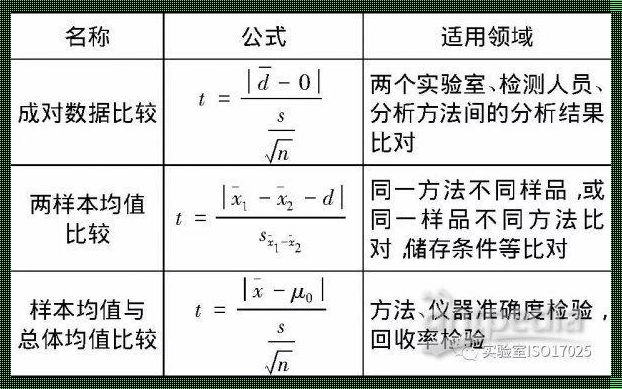
首先，我们需要知道t检验的目的是什么。假设检验通常包括零假设（H0）和备择假设（H1）。在t检验中，零假设通常是指两个样本均值相等，而备择假设是指两个样本均值不等。p值的计算就是基于这个零假设进行的。

接下来，我们需要了解正态分布。正态分布是一种常见的连续概率分布，它具有对称性和 bell-shaped 曲线的特点。在实际应用中，我们通常假设样本数据服从正态分布。p值就是指在零假设为真的情况下，观察到的样本数据或更极端数据出现的概率。

计算p值的方法有很多种，但最常用的方法是累积分布函数（CDF）法。具体步骤如下：

1. 计算样本均值和样本标准差。
2. 计算t统计量：t = (样本均值1 - 样本均值2) / √[(s1^2 / n1) + (s2^2 / n2)]，其中s1和s2分别是两个样本的标准差，n1和n2分别是两个样本的大小。
3. 利用t分布表或计算机软件查找对应的t临界值。这个临界值与显著性水平（通常取0.05或0.01）和自由度（df = n1 + n2 - 2）有关。
4. 计算p值：p = P(T > t)，其中T是t分布的随机变量。

在这里，我们需要注意两点：一是p值是一个概率值，它的取值范围在0到1之间；二是p值越小，拒绝零假设的证据越充分。一般来说，当p值小于显著性水平时，我们就有足够的证据拒绝零假设，认为两个样本均值存在显著差异。

总之，t检验的p值计算是一个涉及统计学知识的过程。掌握好相关概念和计算方法，就能更好地应用于实际问题中。在这个过程中，我们不仅要关注计算过程，还要关注结果背后的意义，从而为决策和分析提供有力支持。