线性空间，这个充满神秘色彩的数学领域，令人着迷。在这个领域中，n维线性空间的维数问题，如同一片未知的世界，等待着我们去探索。

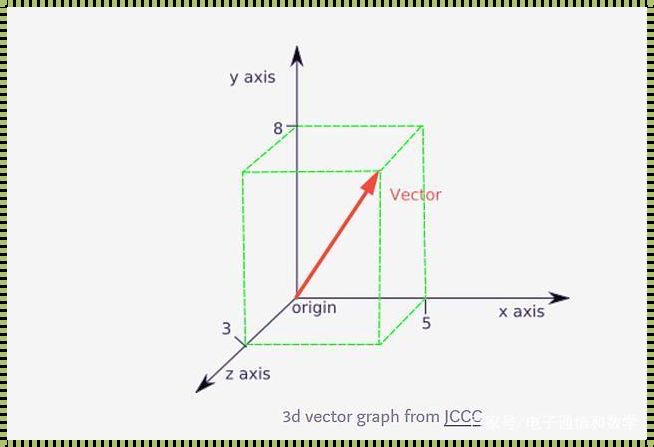
“维度”，这个词似乎充满了魔力，让人陷入无尽的遐想。我们在生活中所熟悉的三维空间，是我们 daily life 的基础。但是，当维度数量增加，我们所面对的世界将变得愈发神秘。

“n维线性空间的维数”，这个看似复杂的问题，其实有着简单的解释。想象一下，我们在二维平面上画一个点，这个点在平面上的位置可以用两个坐标来描述：x坐标和y坐标。当我们从二维平面上升到三维空间，我们需要三个坐标来描述一个点：x坐标、y坐标和z坐标。以此类推，n维空间中的一个点，需要n个坐标来描述。因此，n维线性空间的维数，就是其所需坐标数量的维度。

然而，这个简单的解释却隐藏着深邃的数学原理。在n维空间中，每个维度都代表着一种可能的方向。我们可以沿着这些方向自由地移动，探索这个未知的世界。这个世界的奥秘，不仅仅在于其维度的数量，更在于这些维度之间的相互关系。

“惊现”，这个词似乎在向我们暗示，n维线性空间的维数问题，还有许多未知等待我们去发现。或许，在我们探索这个问题的过程中，我们会惊奇地发现，原来我们生活在一个充满可能性的世界中。

在这个未知的世界中，我们既是探索者，也是发现者。我们用数学的眼光去审视这个世界，用逻辑的思维去解析这个问题。我们相信，只要我们持之以恒，我们终将揭开这个问题的神秘面纱。

线性空间的问题，不仅仅是数学问题，更是一个哲学问题。它让我们思考，我们的世界究竟是怎样的？我们的认知是否有限？这些问题，或许永远没有答案，但正是这些问题的存在，激发了我们对未知世界的探索欲望。

总的来说，n维线性空间的维数问题，是一个充满神秘色彩的问题。它让我们思考，让我们惊现未知的世界。在这个问题中，我们既是探索者，也是发现者。我们相信，只要我们持之以恒，我们终将揭开这个问题的神秘面纱。