Beta分布是一种连续概率分布，它在统计学中有着广泛的应用。它的概率密度函数具有独特的性质，可以用来描述许多实际问题中的随机变量。

Beta分布的概率密度函数可以表示为：

f(x;a,b) = x^(a-1) * (1-x)^(b-1) / [B(a,b)]

其中，a和b是Beta分布的形状参数，B(a,b)是Beta函数，它与a和b有关。

这个概率密度函数有几个重要的性质：

1. 归一性：Beta分布的概率密度函数在整个实数轴上的积分等于1，这意味着概率密度函数的总概率为1。

2. 对称性：Beta分布的概率密度函数关于x=0.5对称，即f(x;a,b) = f(1-x;b,a)。

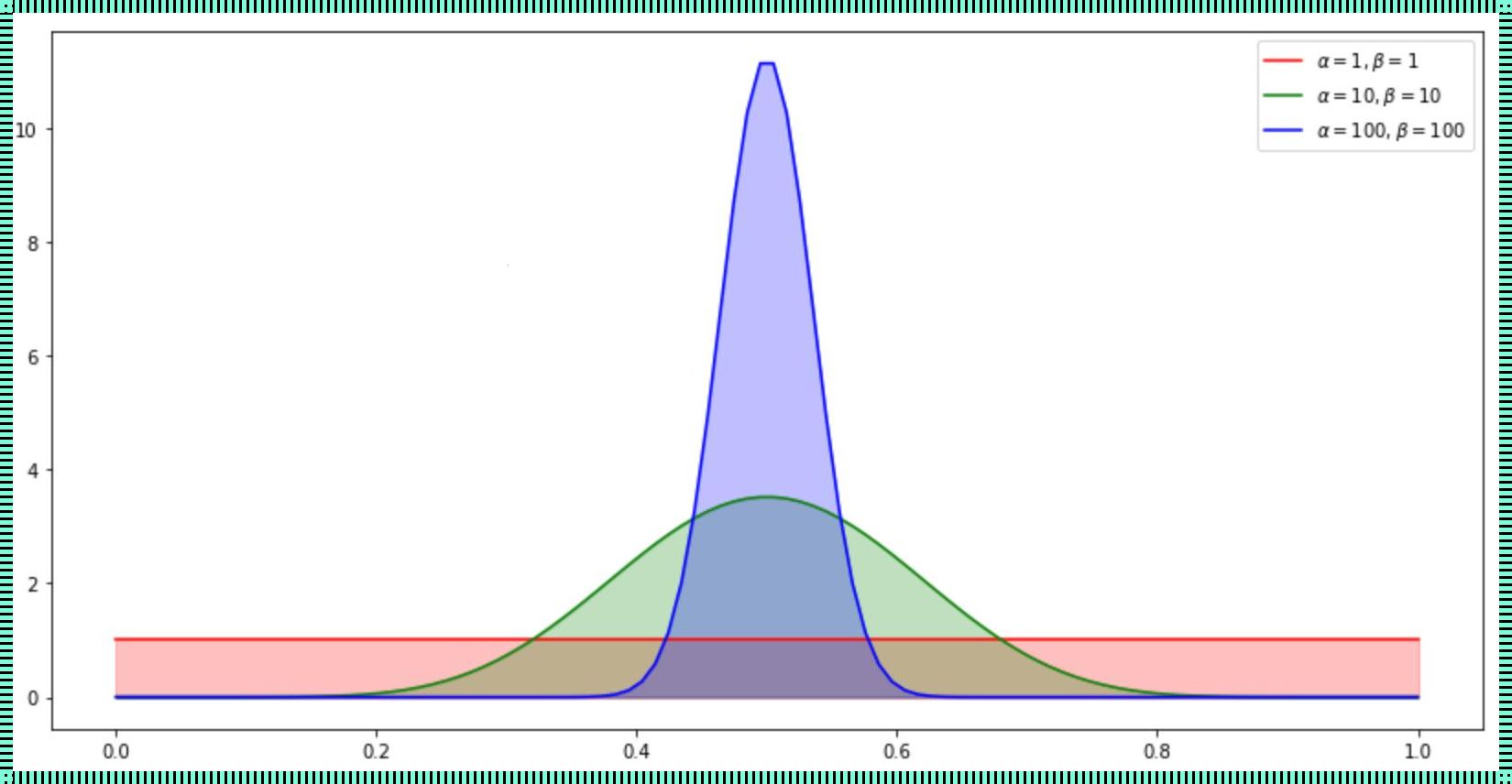
3. 凹凸性：当a>1时，概率密度函数在x=0.5处取得最大值，且在x=0和x=1时趋于0。当a<1时，概率密度函数在x=0处取得最大值，且在x=0.5和x=1时趋于0。当a=1时，概率密度函数在x=0和x=1时取得相同的值，且在x=0.5处取得最大值。

4. 渐进性：当a和b都很大时，Beta分布的概率密度函数在x=0.5处趋于正态分布的概率密度函数。

通过这些性质，我们可以更好地理解和应用Beta分布。例如，在实际问题中，当我们需要描述一个随机变量，它的取值范围在0和1之间，且具有一定的凹凸性时，我们可以考虑使用Beta分布来建模这个随机变量。

Beta分布的概率密度函数在实际应用中具有很大的灵活性，可以通过调整形状参数a和b来适应不同的数据和场景。这使得Beta分布成为一种非常实用的概率分布，可以帮助我们更好地理解和描述现实世界中的随机现象。