“正四棱柱，你知道它的面积和体积公式吗？”小明问。

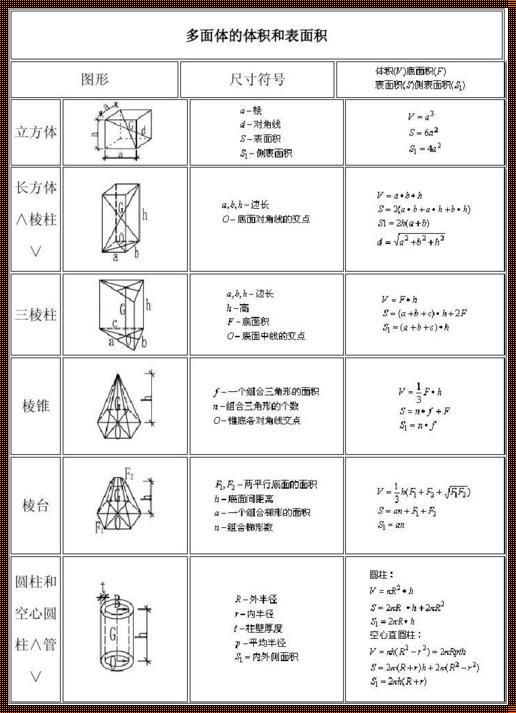
“当然知道，面积公式是$A = 6a^2$，体积公式是$V = a^3$。”小华回答。

“那你知道为什么这两个公式是这样的吗？”小明继续问。

小华犹豫了一下，说：“这个，我就不知道了。”

这就是我们今天要探讨的问题：正四棱柱的面积和体积公式是如何得出的，以及它们背后的数学原理。

首先，我们来回顾一下正四棱柱的定义。正四棱柱是一个底面为正方形，顶面也为正方形，侧面为四个矩形的立体图形。它的六个面都是矩形，其中底面和顶面是相等的正方形。

那么，面积和体积的公式是如何得出的呢？

我们先来看面积公式$A = 6a^2$。这个公式实际上是正四棱柱六个矩形面积之和。其中，底面和顶面的面积都是$a^2$，因为它们是正方形。而四个侧面的面积都是$2a \times h$，其中$h$是正四棱柱的高。所以，六个矩形面积之和就是$2a^2 + 2a \times h + 2a \times h + 2a \times h = 6a^2$。

接下来，我们来看体积公式$V = a^3$。这个公式实际上就是正四棱柱的体积公式。因为正四棱柱的底面是一个正方形，边长为$a$，所以底面的面积就是$a^2$。而正四棱柱的高也是$a$，所以体积就是底面面积乘以高，即$V = a^2 \times a = a^3$。

通过以上的解释，我们可以看到，正四棱柱的面积和体积公式并不是凭空出现的，而是基于它的几何特征和数学原理得出的。这也体现了数学的美妙和严谨，通过对图形的深入理解和分析，我们可以得出简洁而优雅的公式。

然而，面积和体积公式只是正四棱柱几何特征的一种表达方式，还有许多其他的数学性质和公式可以描述它。比如，正四棱柱的对角线长度、表面积、侧面积等，都可以通过相应的公式来计算。这些公式不仅可以帮助我们更好地理解和描述正四棱柱，还可以应用于实际问题中，比如建筑设计、物体制造等领域。

“原来正四棱柱的面积和体积公式是这样的！”小明和小华的对话让我深思。

面积和体积公式只是数学世界中的一小部分，但它们却揭示了数学的奥秘和美丽。通过学习和探索，我们可以更深入地理解数学，发现更多的公式和性质，让我们的生活更加美好。

“数学，真是神奇而美妙！”我感慨道。