正三棱锥，这一几何图形独特而神秘，自古以来便引起了许多数学家和几何学家的浓厚兴趣。它的独特性质和广泛应用，使其在数学、物理、工程等领域中占据了一席之地。今天，我们将深入探讨正三棱锥的表面积和体积公式，以期对其有更为全面的了解。

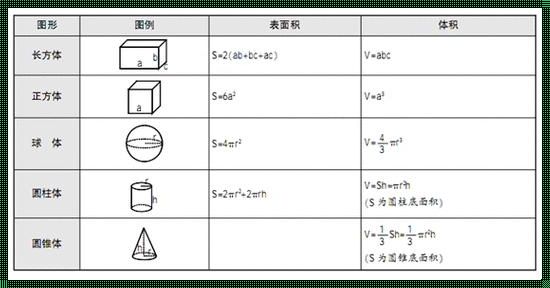
首先，让我们回顾一下正三棱锥的定义。正三棱锥是一个底面为等边三角形，顶点在底面上的四面体。其底面三角形的三边相等，三个顶角均为60度。设正三棱锥的底面边长为a，高为h，侧棱长为l。

接下来，我们来探讨正三棱锥的表面积公式。正三棱锥的表面积由底面积和三个侧面积组成。底面积为等边三角形面积，可用公式计算：底面积 = (a^2 √3) / 4。侧面积则可看作是一个等腰三角形，其面积为(1/2 l h)。因此，正三棱锥的表面积公式为：表面积 = 底面积 + 3 侧面积 = (a^2 √3) / 4 + 3 (1/2 l h)。

然后，我们来解析正三棱锥的体积公式。正三棱锥的体积由底面积和高决定。根据底面积公式，我们已经得到了底面积。因此，正三棱锥的体积公式为：体积 = (1/3 底面积 高) = (1/3 (a^2 √3) / 4 * h)。

通过上述推导，我们得到了正三棱锥的表面积和体积公式。然而，这些公式背后的几何意义和应用价值仍值得我们深入探讨。例如，在工程领域，正三棱锥的体积公式可以用于计算三棱锥形沙堆的体积，从而为施工提供准确的数据。在数学领域，正三棱锥的表面积和体积公式可以作为教学实例，帮助学生更好地理解和掌握几何学的相关知识。

总之，正三棱锥的表面积和体积公式是我们理解和应用这一几何图形的基础。通过深入探讨和解析这些公式，我们可以更好地了解正三棱锥的性质，并将其应用于各个领域。希望本文能为您对正三棱锥的理解提供新的视角和启示。