正四棱锥，一种简单而优雅的几何形状，其内切球体积的研究，既是对数学深度的探索，也是对几何之美的挖掘。

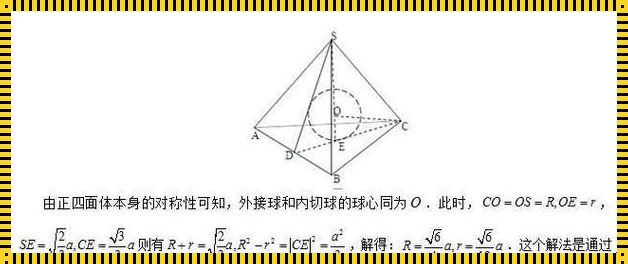
当我们谈论正四棱锥的内切球时，我们实际上是在探讨一个几何体的内部结构。这个内切球，是这个四棱锥的中心点，并且球面与四棱锥的各个面都相切。这个球的大小，直接影响了四棱锥的几何特性。

我们可以通过数学公式来计算这个内切球的体积。假设四棱锥的底面边长为a，高为h，那么内切球的半径r可以通过以下公式得出：r = (ah)/(2sqrt(2a^2 + h^2))。然后，我们就可以用球的体积公式V = (4/3)pi*r^3 来计算内切球的体积。

这个计算过程，是对数学公式的运用，也是对数学逻辑的探索。每一步的推导，都是对数学深度的理解。然而，这个内切球的体积，不仅仅是数学公式上的数字，它更是几何之美的一部分。

内切球的体积，影响了正四棱锥的形状和结构。当内切球的体积增大时，四棱锥的顶部会变得更加尖锐；当内切球的体积减小时，四棱锥的顶部会变得更加平坦。这种变化，正是几何之美的体现，同时也是数学的魅力所在。

我们探索正四棱锥内切球的体积，不仅是为了理解数学公式，更是为了挖掘几何之美，探索数学的深度。每一个几何形状，都有其独特的内部结构，都有其独特的数学之美。通过计算和探索，我们可以更深入地理解这种美，更深刻地感受数学的魅力。

在这个过程中，我们也在不断地挑战自己，提升自己的数学能力。每一次的计算，都是对数学逻辑的理解；每一次的探索，都是对几何之美的挖掘。我们期待在这个过程中，找到数学的魅力，找到几何之美。