在图论中，二分图是一种特殊的图，其所有顶点可以被分成两个不相交的集合，并且图中的每条边的两个顶点分别属于这两个不同的集合。而基数环，是指一个环形图中，每个顶点都有一个唯一的整数标识，且标识的顺序满足环的顺序，即对于环中的任意一条边(u, v)，顶点u的标识小于顶点v的标识。

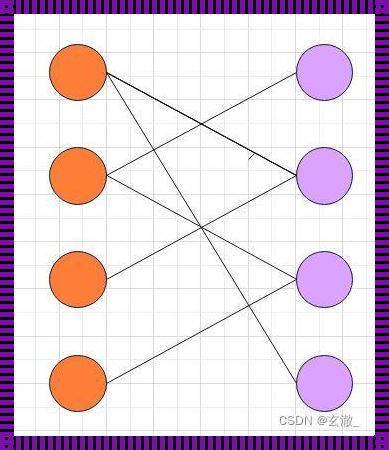
那么，为什么二分图不存在基数环呢？

首先，我们需要了解二分图的性质。由于二分图的特殊性，其所有的边都连接两个不同的集合的顶点。这就意味着，在二分图中，不可能存在一个顶点，其所有相邻的顶点的标识都小于或等于它自己的标识。因为如果存在这样的顶点，那么它必然与属于同一集合的其它顶点相连，这与二分图的定义矛盾。

其次，我们来看基数环的定义。基数环要求每个顶点都有一个唯一的整数标识，且标识的顺序满足环的顺序。在二分图中，由于顶点被分成两个不相交的集合，因此无法为每个顶点分配一个唯一的整数标识，使得标识的顺序满足环的顺序。因为在任意一个环中，都存在一个顶点，其相邻的顶点的标识都小于或等于它自己的标识，这在二分图中是不可能实现的。

综上所述，二分图不存在基数环。这是因为二分图的特殊性质决定了其无法满足基数环的定义要求。