图论作为数学领域中一个重要的分支，研究的是图的结构和性质。在图论中，完全二部图和哈密尔顿图是两个非常有趣且重要的概念。本文将深入探讨这两个概念，以揭示它们之间的奥秘。

首先，让我们来看看完全二部图。完全二部图是一个特殊的图，它由两个不同的顶点集合V1和V2组成，并且V1中的每个顶点都与V2中的每个顶点相连。换句话说，完全二部图是一个二元组(V1, V2)，其中V1和V2是两个不相交的集合，并且对于任意的u∈V1和v∈V2，都存在一条边(u, v)。这种图可以看作是两个集合之间的完全映射，也可以看作是一种二分化的结构，其中V1和V2分别代表了两个不同的“类型”或“集合”。

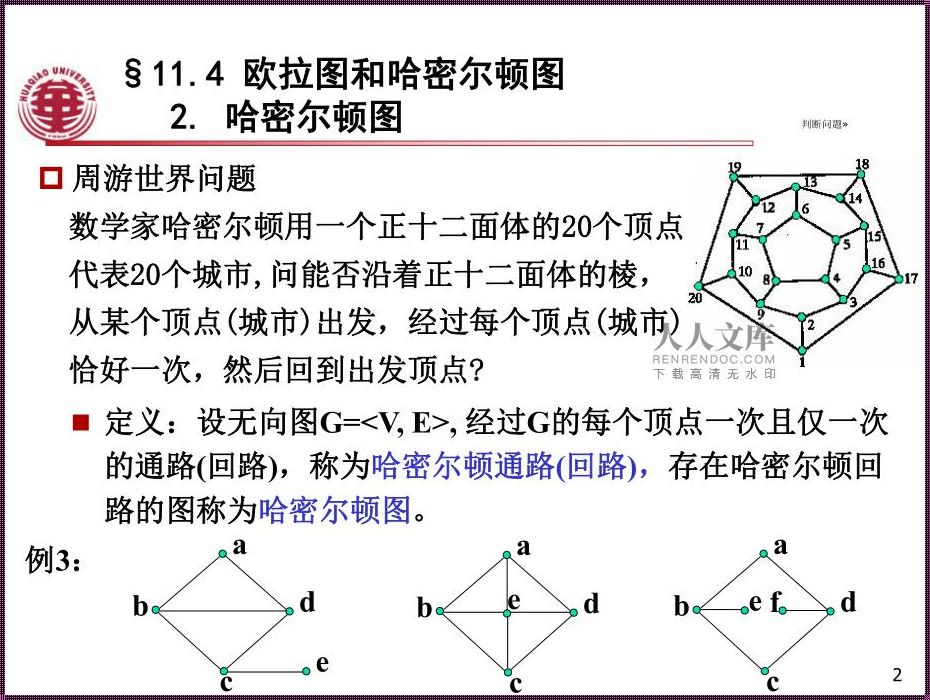
接下来，我们来看看哈密尔顿图。哈密尔顿图，又称哈密尔顿回路图，是一种特殊的图，它具有一条特殊的路径，称为哈密尔顿路径。这条路径经过图中的每个顶点恰好一次，并且最后回到起点。换句话说，哈密尔顿图是一个有n个顶点的图，其中存在一条路径，它经过每个顶点一次，并且最后回到起点。这种图可以看作是一种遍历所有顶点的路径，也可以看作是一种具有环形结构的图。

现在，让我们来探讨一下完全二部图是否是哈密尔顿图。对于一个完全二部图，我们可以将它看作是由两个集合组成的，每个集合中的顶点都与其他集合中的顶点相连。如果我们尝试在这个完全二部图上寻找一条哈密尔顿路径，我们会发现，由于两个集合之间的顶点都是相连的，因此可以很容易地找到一条经过每个顶点一次并且最后回到起点的路径。因此，我们可以得出结论：完全二部图是哈密尔顿图。

通过以上的探讨，我们可以发现，完全二部图和哈密尔顿图之间存在着密切的关系。这种关系揭示了图论中的一些奥秘，也为我们进一步研究图的结构和性质提供了新的思路。

总之，完全二部图和哈密尔顿图是图论中的两个重要概念。通过深入探讨它们之间的奥秘，我们可以更好地理解图的结构和性质，也为图论领域的研究提供了新的方向。