在教育的道路上，我们总是不断地探索和学习。而数学作为一门基础学科，其内在的规律和奥妙也一直吸引着我们去深入挖掘。今天，我们就来谈谈一个看似简单，却蕴含着丰富内涵的数学概念——反正切函数的单调性。

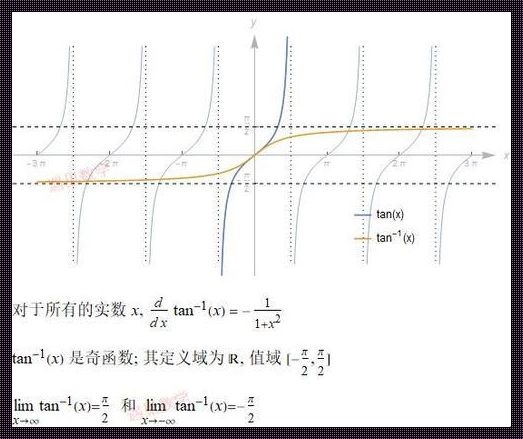
首先，让我们来了解一下什么是反正切函数。反正切函数，简称arctan，是三角函数的一种，定义为正切函数的反函数。换句话说，反正切函数就是将正切函数的值映射回原来的自变量。我们知道，正切函数是一个周期性的函数，其周期为π。而反正切函数的图像则是一条与x轴相交于点(1,0)的曲线。

那么，反正切函数的单调性又是什么呢？简单来说，单调性是指一个函数在其定义域内是否具有单调递增或单调递减的性质。对于反正切函数来说，它在区间(-π/2, π/2)上具有单调递增的性质。这意味着在这个区间内，随着自变量的增加，反正切函数的值也在逐渐增大。而在区间(π/2, 3π/2)上，反正切函数则具有单调递减的性质。也就是说，在这个区间内，随着自变量的增加，反正切函数的值却在逐渐减小。

那么，为什么我们要关注反正切函数的单调性呢？这是因为在教育中，数学不仅仅是一门科学，更是一种思维方式。通过研究反正切函数的单调性，我们可以培养自己的逻辑思维能力、分析问题的能力以及解决问题的能力。而这些能力对于我们在学习和生活中遇到的各种问题都是非常重要的。

首先，通过研究反正切函数的单调性，我们可以锻炼自己的逻辑思维能力。在研究过程中，我们需要对反正切函数的定义、性质以及图像进行深入的分析从而得出其单调性的结论。这个过程需要我们运用严密的逻辑推理不断提出假设验证假设并得出结论这对于培养我们的逻辑思维能力是非常有帮助的。

其次，通过研究反正切函数的单调性我们可以提高自己的分析问题的能力。在研究过程中我们需要对反正切函数的定义域值域以及单调区间进行分析从而得出其单调性的结论。这个过程需要我们运用严谨的数学分析方法不断地对问题进行拆解归纳和总结这对于提高我们的分析问题的能力是非常有帮助的。

最后通过研究反正切函数的单调性我们可以增强自己的解决问题的能力。在研究过程中我们需要运用所学的数学知识如导数极限等来证明反正切函数的单调性。这个过程需要我们运用创新的思维方式不断地尝试新的方法新的技巧来解决难题这对于增强我们的解决问题的能力是非常有帮助的。

总之反正切函数的单调性虽然看似简单但其背后所蕴含的数学奥秘和教育价值却是非常丰富的。通过研究反正切函数的单调性我们可以培养自己的逻辑思维能力分析问题的能力以及解决问题的能力。而这些能力对于我们在学习和生活中遇到的各种问题都是非常重要的。因此让我们一起在数学的世界里探索更多的奥秘吧！