在数学的海洋中，有一种神秘的函数，它如同夜空中的繁星，闪烁着智慧的光芒。这种函数就是我们今天要探讨的主题——正割函数。正割函数，又称为secant函数，是三角函数的一种，它在数学、物理、工程等领域都有着广泛的应用。那么，正割函数究竟有着怎样的魅力呢？让我们一起来揭开它的神秘面纱。

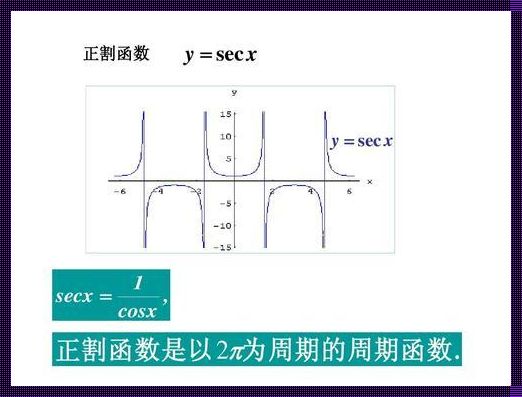
首先，我们来了解一下正割函数的定义。在直角三角形中，正割函数是指对边与斜边的比值。用符号表示为：secθ=1/cosθ。从这个定义中，我们可以看出正割函数与余弦函数之间存在着密切的联系。实际上，正割函数和余弦函数可以互相推导，它们共同构成了三角函数的基本框架。

接下来，我们来看看正割函数的性质。正割函数具有以下性质：

1. 定义域：正割函数的定义域为全体实数。这意味着我们可以在任何实数范围内使用正割函数进行计算和分析。

2. 值域：正割函数的值域为全体实数。这使得正割函数具有广泛的适用性，可以描述各种不同类型和规模的现象和问题。

3. 周期性：正割函数没有周期性。这与三角函数中的其他成员不同，例如正弦函数和余弦函数都具有周期性。这使得正割函数在某些情况下更加灵活和方便使用。

4. 奇偶性：正割函数是奇函数，即sec(-θ)=-secθ。这意味着正割函数在对称轴处取得零点，并且关于原点对称。这一性质使得我们可以利用正割函数来解决一些与对称性相关的问题。

5. 导数：正割函数的导数为secθtanθ。这一性质使得我们可以利用导数来计算正割函数的变化率和斜率，从而更好地理解和分析各种现象和问题。

6. 不定积分：正割函数的不定积分为ln|secθ+tanθ|+C。这一性质使得我们可以利用不定积分来计算正割函数的原函数，从而更好地理解和分析各种变化和累积效应。

7. 定积分：正割函数的定积分为∫secθdx=ln|secθ+tanθ|+C。这一性质使得我们可以利用定积分来计算正割函数的面积和体积，从而更好地理解和分析各种空间和形态特征。

这些性质为我们进一步研究正割函数提供了基础。在实际应用中，正割函数可以帮助我们解决许多复杂的问题。例如，在物理学中，正割函数可以用来描述振动、波动等现象；在工程学中，正割函数可以用来计算角度、长度等参数；在计算机科学中，正割函数可以用来处理图像、数据等对象。可以说，正割函数在各个领域都有着广泛的应用。

然而，正如任何工具一样，正割函数并非完美无缺。在实际应用中，我们常常会遇到一些困难和挑战。例如，由于正割函数的周期性在某些情况下难以直接应用；由于正割函数的不定积分和定积分涉及到了对数、绝对值等复杂运算，给计算带来了一定的难度。因此，我们需要不断地探索和研究，以克服这些困难，更好地利用正割函数来解决实际问题。

在这个过程中，我们可以借鉴其他领域的经验和方法。例如，我们可以利用泰勒级数来近似计算正割函数的值；我们可以利用数值方法来求解正割函数的不定积分和定积分；我们可以利用复数理论来简化正割函数的运算。通过这些方法，我们可以更好地理解和掌握正割函数，为实际应用提供有力的支持。

总之，正割函数是一种神奇的数学工具，它在数学、物理、工程等领域都有着广泛的应用。虽然正割函数在实际应用中存在一定的困难和挑战，但通过不断地探索和研究，我们可以克服这些困难，更好地利用正割函数来解决实际问题。让我们携手共进，探索数学之美，创造更加美好的未来！