在我国数学领域，反正切函数（arctan）是个颇具神秘色彩的函数。它与正切函数（tan）息息相关，却有着截然不同的性质。正切函数是无界函数，那幺，反正切函数是否有界呢？

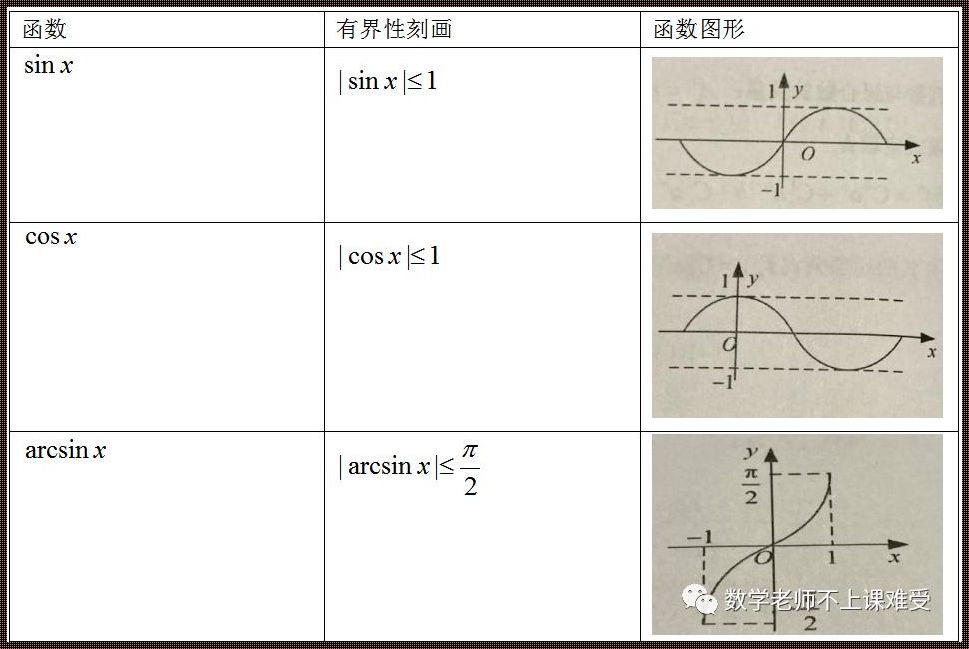
一、反正切函数的定义与性质

我们先来了解一下反正切函数的定义。设y = arctan(x)，则x = tan(y)。反正切函数的定义域为实数集，值域为(-π/2, π/2)。它是一种奇函数，图像关于原点对称。

二、反正切函数的有界性探究

1. 反正切函数的单调性

我们可以通过求导来分析反正切函数的单调性。求导得：dy/dx = 1/((1+x^2)^(3/2))。当x > 0时，dy/dx > 0，说明反正切函数在（0，+∞）上单调递增；当x

2. 反正切函数的极限

我们可以通过求极限来判断反正切函数的有界性。当x趋近于0时，arctan(x)趋近于0；当x趋近于正无穷时，arctan(x)趋近于π/2；当x趋近于负无穷时，arctan(x)趋近于-π/2。由此可知，反正切函数的值域为(-π/2, π/2)。

3. 反正切函数的周期性

我们可以通过观察周期性来进一步分析有界性。将x替换为x + π，得到arctan(x + π) = arctan(x)。这说明反正切函数具有周期性，周期为π。因此，我们只需关注一个周期内的有界性。

4. 反正切函数的有界性

在一个周期（π，2π）内，反正切函数的值域为(-π/2，π/2)。我们可以找到一个特殊点，如x = 1，此时arctan(1) = π/4，处于值域边界。由此可知，反正切函数在一个周期内有界。

综上所述，我们可以得出结论：反正切函数是有界函数。但它并非在整个定义域上有界，而是在一个周期内有界。这一特性使得反正切函数在实际应用中有着广泛的价值。

三、反正切函数的应用

1. 三角函数的化简

在解决一些三角问题时，我们可以利用反正切函数将复杂的三角函数化简。例如，设y = sin(3x) + cos(2x)，我们可以通过反正切函数将其化简为y = 2tan(x)。

2. 微分方程的求解

在求解一些微分方程时，我们可以利用反正切函数来简化问题。例如，求解y'' + y = sin(x)的边值问题，可以利用反正切函数得到y = tan(x) + C。

3. 反正切函数在信号与系统中的应用

在信号与系统领域，反正切函数常用于分析周期性信号。通过反正切函数，我们可以将周期性信号分解为不同频率的正弦波和余弦波，进而进行信号处理。

总之，反正切函数作为数学领域的一个神秘函数，既有界又具有广泛的应用。它既不同于正切函数，也独具特色。在未来的研究与应用中，反正切函数将继续绽放光彩。