一、正割余割函数的图像奥秘

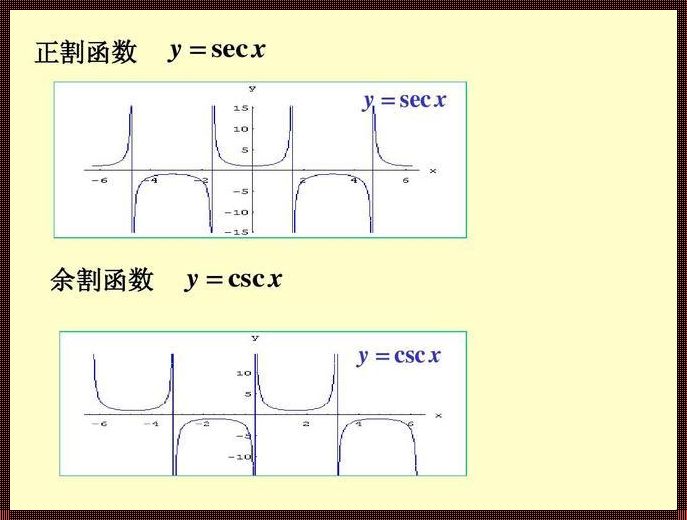
“割”字辈的数学函数，在数学领域里可谓是声名显赫。正割函数和余割函数，作为割圆术的基础，其图像奥秘一直吸引着我们去探索。

正割函数y = sinx，余割函数y = cosx，它们的图像犹如江湖中的双剑合璧，共舞九天。正割函数sinx的图像，起始点为（0，0），随着x的增大，图像向上攀升，至（π/2，1）达到顶峰，然后逐步下滑，至（3π/2，-1）跌落低谷，最后回到（2π，0）。这是一幅极具动态美感的图像，犹如山水画卷中的飞流直下，令人陶醉。

而余割函数cosx的图像，则呈现出另一种韵味。起始点为（0，1），随着x的增大，图像如弧线般下滑至（π，0），接着犹如弹簧般迅速回升，至（2π，1）后又逐步下滑，至（3π，0）结束。这是一幅充满曲线美的图像，如诗如画。

二、正割余割函数图像的数学美学

正割余割函数的图像，不仅具有动态美和曲线美，更蕴含着丰富的数学美学。

首先，它们的图像都是周期性的，符合数学的规律性。正割函数sinx和余割函数cosx的周期均为2π。这种周期性在图像上表现为，当x增加或减少2π时，图像会重复之前的走势。

其次，正割函数和余割函数的图像在坐标系中呈现出一种对称美。sinx和cosx的图像关于y轴对称，即对于任意x，sinx = cos(-x)和cosx = sin(-x)。这种对称美体现了数学的和谐性。

最后，正割函数和余割函数的图像还体现了数学的简洁美。它们的公式简单易懂，图像走势直观明了，内涵丰富。

三、正割余割函数图像的启示

正割余割函数的图像，如同数学江湖中的缩影，启示着我们去探寻数学的魅力。它们告诉我们，数学不仅是一门学科，更是一种美学，一种艺术。正如著名数学家陈省身在谈及数学美学时所言：“数学是自由的，数学是美的，数学是有趣的。”

通过对正割余割函数图像的探究，我们不仅能感受到数学的动态美、曲线美、对称美和简洁美，更能体会到数学的无穷魅力。正如江湖传言：“数学之美，不可言说，唯有亲身体验，方能深知。”

总结：正割余割函数的图像之美，犹如数学江湖中的一幅画卷，展现了数学的无穷魅力。让我们沿着这幅画卷，继续探寻数学的奥秘，感受数学的美与乐趣。