海瑟矩阵，这个名称在数学的世界中或许并不像勾股定理或者欧拉公式那样为人所熟知，但它却以一种独特的方式，以其性质震惊了数学界。

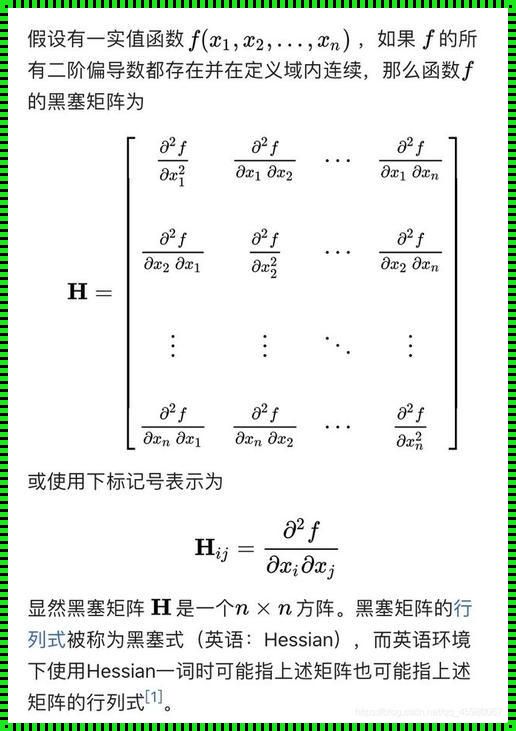
海瑟矩阵，又称补集矩阵，是线性代数中的一类特殊矩阵。它的一个重要性质是，任何一个矩阵都可以通过对其进行行变换和列变换转化为海瑟矩阵。这种性质，仿佛为矩阵的世界打开了一扇新的大门，使得我们可以从一个新的视角去理解和研究矩阵。

海瑟矩阵的另一个性质是，它的对角线元素都是非负的。这一性质，不仅使得海瑟矩阵在数学理论的研究中占有重要的地位，同时也使其在工程和计算机科学等领域有着广泛的应用。

然而，海瑟矩阵的最大惊现之处，还是在于它的独特性质——任何一个矩阵都可以通过一系列的行和列操作转化为海瑟矩阵，这一性质不仅使得海瑟矩阵成为了矩阵理论研究的一个重要工具，同时也为矩阵的计算和优化提供了一种新的方法。

在这个数学的世界中，海瑟矩阵就像一位默默无闻的英雄，以其独特的性质和作用，为数学的发展做出了巨大的贡献。它的出现，不仅让我们对矩阵的理解更加深入，也让我们对数学的世界充满了惊奇和期待。

正如数学家陈景润所说：“数学之美，在于它的逻辑性和严谨性，更在于它的惊奇和惊喜。”海瑟矩阵的性质，正是这种惊奇和惊喜的最好体现。