在数学的世界里，有许多看似简单的命题，背后却蕴藏着深邃的哲理。今天，我要和大家探讨的便是这样一个命题：“函数可导则导函数可积”。

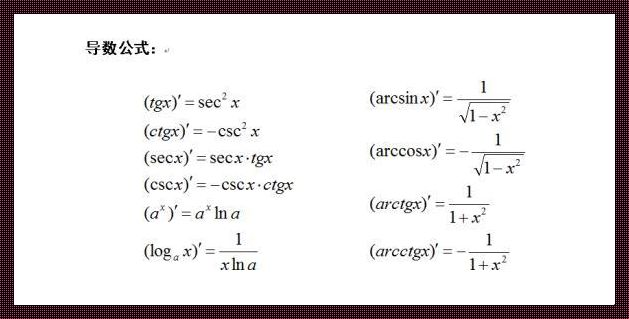
首先，让我们来解释一下这个命题中的几个关键词。函数，是数学中的一个基本概念，它描述了一种输入和输出之间的映射关系。可导，意味着函数在某一点的导数存在，导数是函数图像的斜率，反映了函数在该点的变化趋势。而导函数，则是原函数的导数，它描述了原函数的变化率。可积，则意味着函数在一个区间内的积分存在，积分是函数图像与x轴之间区域的面积，反映了函数在该区间内的累积效果。

那么，为什么说“函数可导则导函数可积”呢？这其实是因为可导性保证了函数的连续性，而连续性则是可积性的重要条件。我们可以想象，一个函数如果在某一点不可导，那么它在这一点附近的图像就会发生突变，就像是一个突然断裂的曲线。这样的函数，其导函数在这一点附近的图像就会是一个尖角，无法进行积分。因此，一个不可导的函数，其导函数自然也就不可积。

然而，这并不意味着所有的可导函数的导函数都一定可积。事实上，只有当原函数在某一区间内满足一定条件时，其导函数才可积。这些条件通常包括单调性、有界性等。但这已经超出了原命题的范畴，我们在这里不再展开讨论。

通过对这个命题的探讨，我们不仅可以更深入地理解函数、导数、积分等基本概念，也可以从中体会到数学的严谨性和美感。在这个看似简单的命题背后，隐藏着数学家们几百年的探索和思考。这也是数学的魅力所在，不是吗？

希望这篇文章能帮助大家更好地理解“函数可导则导函数可积”这一数学命题，也希望大家能从中感受到数学的美丽和魅力。