勒贝格可测集，这是数学中一个重要而深刻的概念。它关乎集合在数学上的可度量性，是实分析中的一个基石。那么，究竟什么是勒贝格可测集呢？

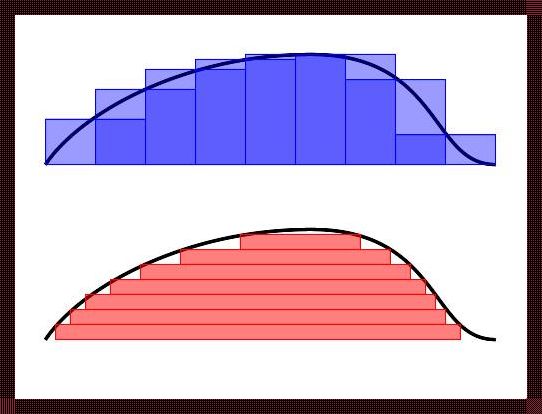
在数学的世界里，勒贝格可测集是一个能够在勒贝格积分下有意义的集合。简单来说，如果我们能够对一个集合进行积分，那么这个集合就是可测的。这听起来似乎有些抽象，让我们通过一个例子来理解。

假设我们有一个区间[0,1]，这个区间的长度是1。我们可以对区间内的任何一个连续函数进行积分，比如函数f(x) = x。我们可以计算这个函数在区间[0,1]上的积分，结果是1/2。这个积分的过程，就是对区间进行度量的过程。在这个过程中，区间[0,1]就是一个勒贝格可测集。

但是，如果我们要度量的是一个不规则的形状，比如一个曲线或者一个不规则的图形，我们就无法直接对其进行积分。这时候，勒贝格可测集的概念就显得尤为重要。它可以让我们在数学上对这样的集合进行度量。

勒贝格可测集的定义，揭示了数学中的一个重要特性：数学不仅仅是冷冰冰的公式和定理，它更是一种度量和理解世界的方式。勒贝格可测集，就是数学家们用来度量和理解集合的一种工具。

然而，勒贝格可测集的定义并非一蹴而就。它是数学家们通过对集合的深入研究，逐步揭示出来的。这个过程，就像是对数学的一次次探索和发现，充满了挑战和困难，但也充满了乐趣和成就感。

总的来说，勒贝格可测集是一个深刻而重要的数学概念。它不仅让我们能够对集合进行度量，更让我们能够更深入地理解和研究数学。