主成分分析是一种常用的数据降维方法，通过将原始数据映射到新的特征空间，使得新的特征之间相互独立，从而达到降维的目的。在这篇文章中，我们将通过一些简单的例题，详细解释主成分分析的原理和应用。

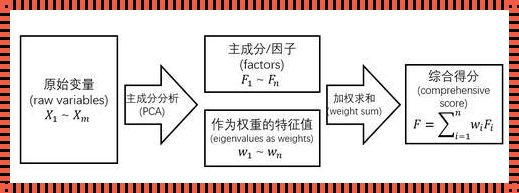
假设我们有一组数据，表示不同学生的成绩，包括数学、英语和物理三个科目。我们可以将这组数据整理成一个矩阵，其中每一行对应一个学生，每一列对应一个科目。接下来，我们可以使用主成分分析的方法，将这个三维数据空间降维到二维或一维。

首先，我们需要计算数据的协方差矩阵，表示不同科目之间的相关性。然后，我们求解协方差矩阵的特征值和特征向量。特征值和特征向量是主成分分析的核心，它们决定了新的特征空间的方向和距离。

接下来，我们根据特征值的大小，选择前两个或前三个特征向量，作为新的特征轴。原始数据在新的特征轴上的投影，就是降维后的数据。这些新的特征轴，就是主成分，它们保留了原始数据的主要信息，同时消除了变量之间的相关性。

通过这个例子，我们可以看到，主成分分析可以将多维数据降维，同时保留数据的主要特征。这种方法在许多领域都有广泛的应用，比如图像处理、机器学习和数据挖掘等。

在实际应用中，我们通常使用一些计算工具，比如Python的scikit-learn库，来完成主成分分析。这个库提供了简单易用的接口，可以帮助我们快速实现主成分分析的功能。

总的来说，主成分分析是一种强大的数据处理方法，通过降维，可以帮助我们更好地理解和分析数据。希望通过这篇文章，你能够更好地理解主成分分析的原理和应用。