"最小元"与"极小元"，这两个词汇在数学的世界里，如同两颗闪耀的星辰，各自散发着独特的光芒。它们在集合论、逻辑学以及计算机科学等领域扮演着至关重要的角色，然而它们之间虽仅有字面上的细微差别，却蕴含着深刻的理念之别。

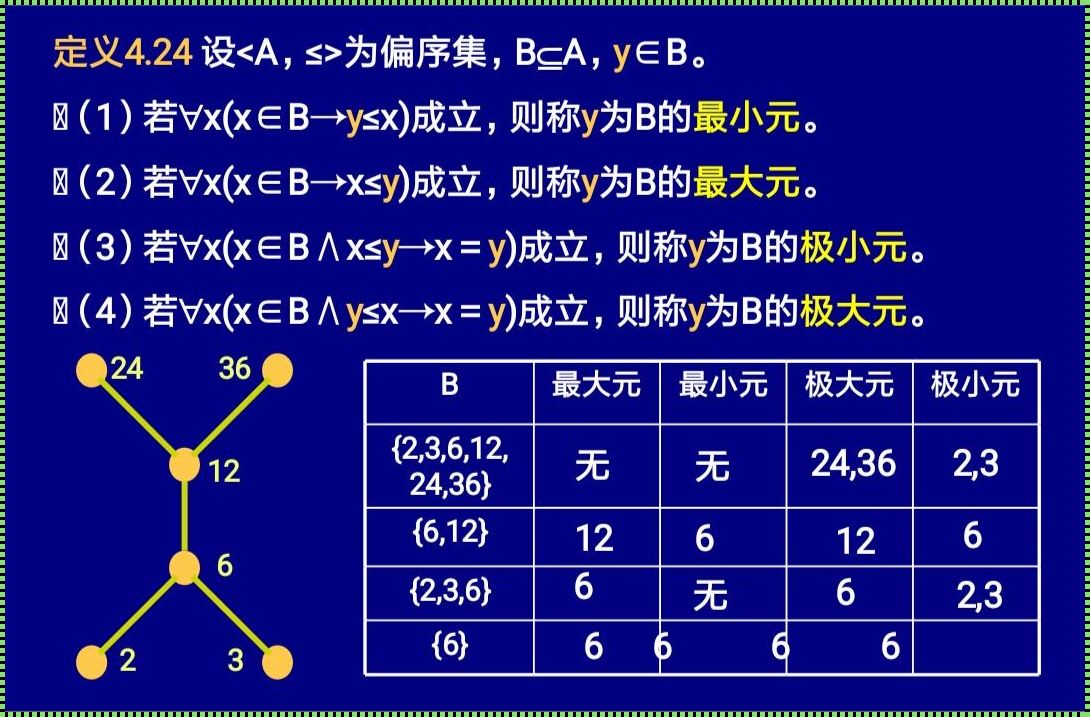
"最小元"一词，常常出现在寻找某种结构或者关系中的最基本、最不可再分元素的语境中。它指的是一种下界，是小于或等于其他所有元素的元素。比如，在数轴上，最小元就是最左端的点，它不具备任何比它更小的属性。在数学的证明中，找到一个最小元，意味着找到了一个足够小的例子，它能够证明某一结论对所有类似的情况都成立。

而"极小元"则有着更加深刻的内涵。在数学的各个分支中，"极小元"往往指的是在给定条件下，具有最小可能的性质或者量度的元素。它不单是一个下界，更是一个局部极值，是一个在某一邻域内不可超越的最小值。在物理学中，极小元常常与能量的最小状态联系在一起，比如在热力学中，一个系统可能达到的最小能量状态，即为其极小元状态。

让我们透过这层神秘的面纱，深入地探究一下这两者的区别。假设我们有一个数学集合，其中包含了许多数字。如果我们说这个集合有一个"最小元"，那么我们找到了一个数字，它是这个集合中最小的，没有比它更小的数字。但是，如果集合中没有最小元，那么我们就不会在这个集合中找到一个确定的数字来作为最小元。

然而，当我们谈论"极小元"时，情况就有所不同了。即使集合中没有最小元，我们仍然可能找到一个"极小元"。这个极小元不一定是真正的最小值，但是它是可达到的，是最接近最小值的元素。在某些数学理论中，极小元的概念是非常重要的，因为它可以给我们提供更多关于集合的信息，帮助我们更深入地理解集合的结构。

为了更好地解释这个概念，让我们回到物理学的例子。假设我们有一个物体，我们想要找到它的最小能量状态。这个最小能量状态就是一个"极小元"，因为它代表了物体能够达到的最小能量水平。在这个状态下，物体不能再减少其能量，除非它发生了一些变化，比如吸收或释放能量。

总之，最小元与极小元的区别在于它们的定义和应用场景。最小元是一个绝对的下界，是无需考虑额外条件的最小值；而极小元是在一定条件下，局部区域内的最小值，它代表了可能达到的最优状态。尽管它们在字面上是如此的接近，但在理论和实践中，它们却有着本质的不同。通过深入理解这些概念，我们能够更好地掌握数学和物理学的精髓，揭示自然界的奥秘。