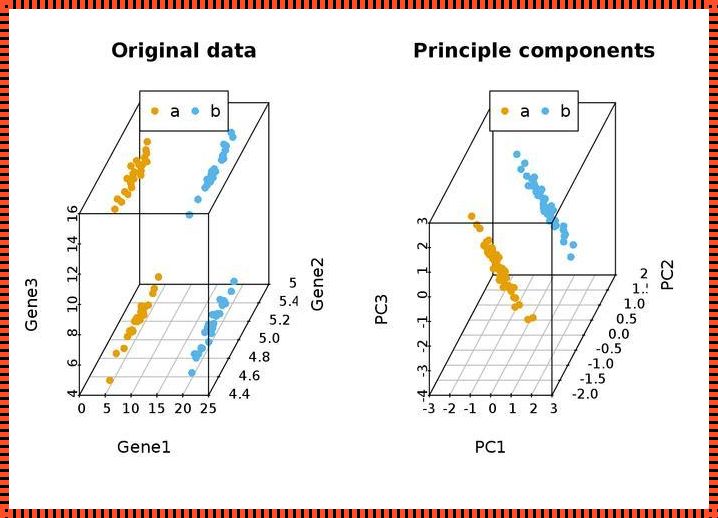
在数据科学的领域中，PCA（主成分分析）是一种强大的工具，它能够帮助我们理解复杂数据背后的结构。PCA通过将原始数据转化为一系列线性不相关的变量，即主成分，来实现数据的降维。这一过程不仅能够简化数据，还能揭示数据中隐藏的模式和关系。

首先，进行PCA分析的第一步是数据预处理。这包括对数据进行标准化或归一化，以确保每个特征的重要性都能够被公平地评估。此外，还需要检查数据中是否存在异常值或缺失值，并对它们进行适当的处理。

接下来，进入PCA的核心步骤——特征值分解。在这个过程中，我们会计算数据的协方差矩阵，并求解特征值和特征向量。协方差矩阵揭示了数据特征之间的相关性，而特征值和特征向量则告诉我们哪些方向上数据的差异最大。

选择主成分的标准有很多，常用的方法是选择前k个最大的特征值对应的特征向量。这些特征向量定义了新的空间，数据在这个新空间中的投影能够保留原始数据的大部分信息。选择k的值是一个平衡的艺术，k值太小会丢失重要信息，而太大则会增加模型的复杂度。

最后，我们将数据转换到新的空间中，即使用选定的主成分来构建新的特征向量。这一步完成了PCA的分析过程，我们现在拥有了一个降维后的数据集，它既简洁又保留了原始数据的关键特征。

PCA的应用范围极其广泛，从图像处理到基因分析，从推荐系统到机器学习，几乎所有需要处理高维数据的领域都有PCA的用武之地。通过PCA，我们能够洞察数据中的模式，发现数据的内在结构，这对于数据的进一步分析和理解至关重要。

在这个过程中，我们不仅仅是简单地减少数据的维度，更重要的是，我们通过PCA揭示出了数据中最重要的信息。这些信息可以帮助我们做出更准确的预测，发现数据之间的隐藏联系，甚至可能会对我们的世界观产生深远的影响。

总的来说，PCA是一种揭示数据背后秘密的钥匙，它让复杂的数据变得简单，让隐藏的模式变得明显。掌握PCA，就是掌握了一种理解世界的新的方式。