在图论中，完全连通子图是一个术语，指的是一种特殊的子图，其中的每两个顶点都是相互连通的。换句话说，如果你想象一个图，完全连通子图就是那个你可以从任何一个顶点出发，通过边到达图中的任何一个其他顶点的部分。

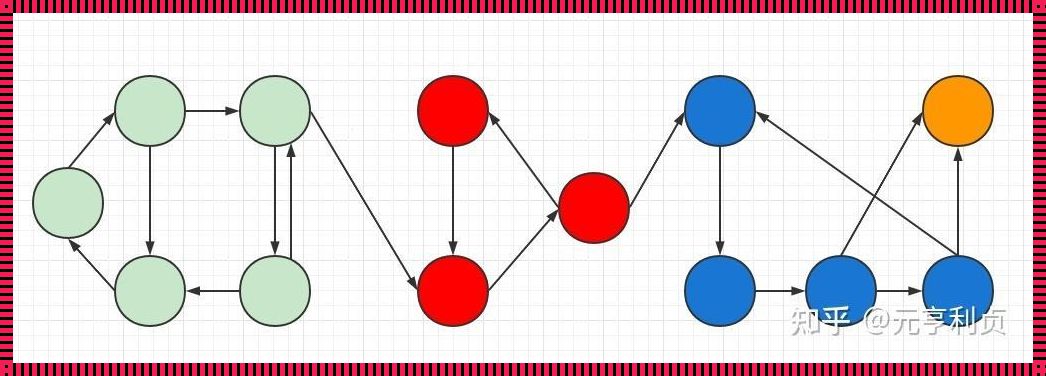
理解完全连通子图的概念，首先要从图的基本概念入手。图是由顶点和边组成的数据结构，顶点可以是任何事物，边则是连接顶点的线或弧。在图中，路径是指从一个顶点到另一个顶点的一系列边的序列，而连通性则是指图中任意两个顶点之间是否存在路径。

当我们说一个子图是“完全连通”的时候，这意味着在这个子图中，无论你选择哪两个顶点，它们之间都有一条路径。这就像是你在一个庞大的网络中，无论你在哪里，你都可以通过一系列的路线到达任何其他地方。

在实际应用中，完全连通子图的概念非常重要。比如，在网络设计中，我们希望网络的任意两个节点之间都能够相互通信，这时，完全连通子图就是我们需要实现的目标。在交通规划中，我们希望城市中的任意两个地点都能够通过道路连接起来，这也涉及到完全连通子图的概念。

掌握完全连通子图的算法是图论中的一个重要课题。有多种算法可以用来寻找一个图中的完全连通子图，其中最著名的是深度优先搜索（DFS）和广度优先搜索（BFS）。这些算法可以帮助我们找到完全连通子图，也可以帮助我们计算完全连通子图的大小，即其中包含的顶点数量。

总的来说，完全连通子图是图论中的一个基本概念，它在理论研究和实际应用中都具有重要意义。通过对完全连通子图的理解和掌握，我们可以更好地解决各种实际问题，优化网络设计，提高交通效率，甚至改进社交网络的构建。