方差，这个在大学统计学中频繁出现的词汇，犹如一串神秘的符号，困扰着许多学生。今天，让我们一起揭开它的面纱，探寻方差背后的故事。

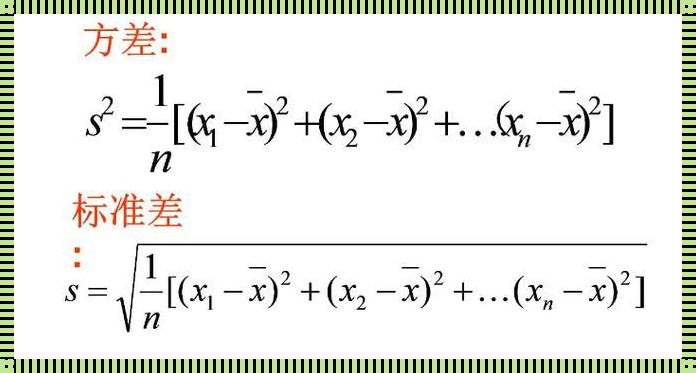
“方差”，一个听起来有些枯燥的词汇，却在生活中扮演着重要的角色。它是一种衡量数据离散程度的统计量，可以描述一组数据的波动大小。换句话说，方差越大，数据的波动性越大，反之亦然。

在大学的学习中，我们经常遇到这样的情况：一组数据呈正态分布，我们需要通过计算方差来了解数据的离散程度。这时，方差的计算公式就派上用场了。常用的方差计算公式如下：

方差 = （Σ(xi - μ)²）/ n

其中，xi 表示数据点，μ 表示平均值，n 表示数据个数。

然而，仅仅掌握方差的计算公式还不够。我们需要深入理解方差背后的含义，才能更好地运用它。方差反映了数据的波动程度，可以帮助我们判断数据的稳定性。在实际应用中，方差小的数据更加稳定，而方差大的数据则存在一定的风险。

当我们提到“方差的计算公式大学”时，我们实际上是在关注大学教育中的一个重要方面：培养学生的统计思维和数据分析能力。在这个信息爆炸的时代，数据分析已成为一门不可或缺的技能。大学教育应引导学生从理论到实践，深入理解方差等统计概念，从而更好地应对未来的挑战。

作为一名大学生，我深知方差等统计知识的重要性。在一次课题研究中，我们小组需要分析一组实验数据。通过计算方差，我们发现数据存在较大的波动性，从而怀疑实验过程中可能存在误差。在进一步的调查中，我们发现了导致波动的原因，并采取了相应的措施加以改进。这次经历让我深刻体会到方差在实际应用中的价值。

总之，方差的计算公式并非枯燥无味，而是蕴含着丰富的统计思想和智慧。大学教育应关注学生对统计知识的理解和应用，培养具备数据分析能力的人才。让我们从方差开始，探索统计学的世界，挖掘数据背后的秘密。

在未来的道路上，我们将继续面临各种挑战。然而，只要我们掌握了方差等基本统计知识，用心去体会和学习，就一定能够应对这些挑战，成为时代的弄潮儿。让我们携手共进，用统计学的力量，开启未来的大门。