当我们谈论t分布时，我们实际上是在讨论一个概率分布，它描述了一个随机变量的可能值及其概率。这个分布有一个形状，它的期望和方差是描述这个分布的两个重要参数。

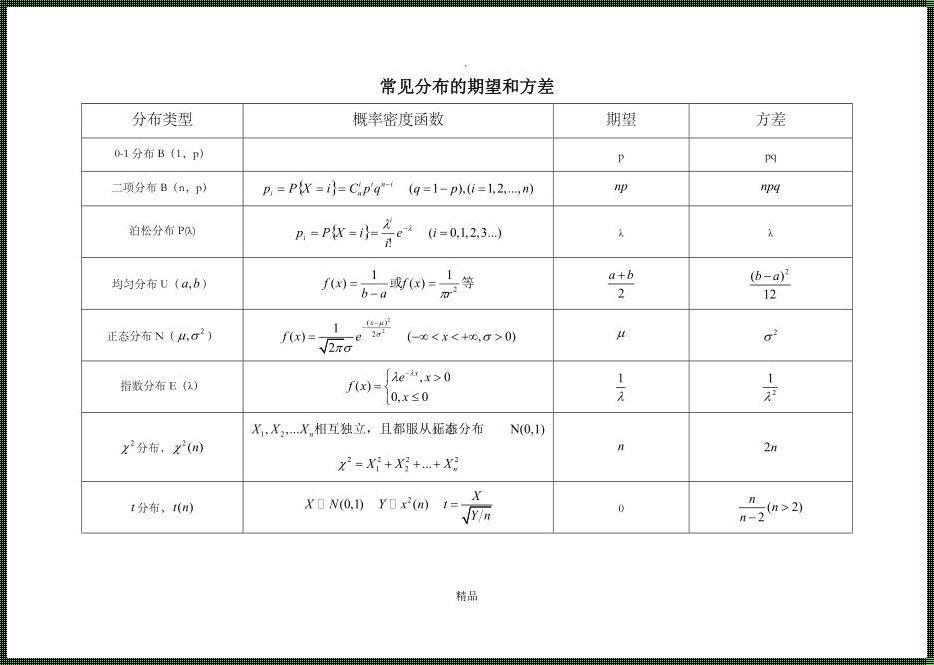
期望是分布的中心位置，它告诉我们随机变量平均会取什么值。在t分布中，期望值等于分布的均值。这意味着，如果我们重复进行多次独立的抽样，并计算每次抽样的平均值，这些平均值的平均将接近于t分布的期望值。

方差是分布的离散程度的度量，它告诉我们随机变量取值的变异程度。在t分布中，方差决定了分布的尾巴的长度。如果方差较小，分布的尾巴较短，表示随机变量取值的变异较小；如果方差较大，分布的尾巴较长，表示随机变量取值的变异较大。

t分布的期望和方差之间的关系是复杂的。期望值决定了分布的中心位置，而方差决定了分布的形状。它们共同决定了随机变量的取值概率分布。

在实际应用中，t分布的期望和方差对于我们理解和分析数据非常重要。例如，在假设检验中，我们常常使用t分布来确定样本均值与总体均值之间的差异是否显著。此时，了解t分布的期望和方差有助于我们正确解释结果。

总之，t分布的期望与方差是理解其概率分布的关键参数。期望值决定了分布的中心位置，方差决定了分布的离散程度。通过深入理解这两个参数，我们能够更好地理解和分析数据，从而在实际应用中做出更准确的决策。