强连通图和强连通分量是图论中的两个重要概念。虽然它们在名称上有相似之处，但它们实际上有着本质的区别。

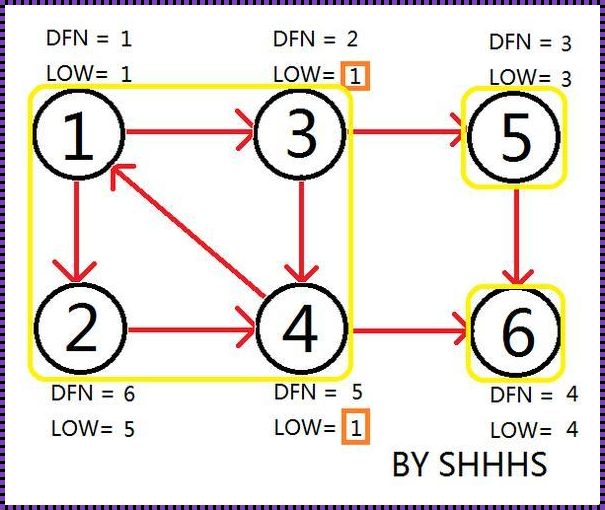
首先，我们来了解一下强连通图。强连通图是指在一个有向图中，任意两个顶点都是相互可达的。也就是说，对于图中的任意两个顶点u和v，都存在一条从u到v的路径和一条从v到u的路径。强连通图的特点是，图中的每个顶点都与其他所有顶点都有直接或间接的连接。

而强连通分量则是强连通图的一个子图。强连通分量是指在一个有向图中，包含所有从一个顶点可以到达的其他顶点的子图。换句话说，强连通分量是由一组相互可达的顶点组成的最大子图。在强连通分量中，任意两个顶点都是相互可达的，且不存在与其他顶点不相互可达的顶点。

简单来说，强连通图是一个整体的属性，描述的是图中所有顶点之间的关系。而强连通分量是一个局部的属性，描述的是图中一个子集的顶点之间的关系。

举个例子来说明这两个概念的区别。假设有一个有向图，包含四个顶点A、B、C和D。如果顶点A可以通过路径到达顶点B、C和D，同时顶点B、C和D也可以通过路径到达顶点A，那么这个有向图就是一个强连通图。在这个强连通图中，如果我们将顶点B和顶点C之间的边删除，那么顶点B和顶点C就形成了一个强连通分量，因为它们之间仍然可以通过其他路径相互可达。

总结一下，强连通图和强连通分量的区别在于它们的定义和描述的范围不同。强连通图描述的是整个图中所有顶点之间的关系，而强连通分量描述的是图中一个子集的顶点之间的关系。这两个概念在图论中起着重要的作用，帮助我们更好地理解和分析图的结构和性质。