三次样条插值是一种在给定的数据点上构建三次多项式函数的方法，以便在这些点之间的任意位置精确地计算函数值。这个过程可以分为以下几个基本步骤：

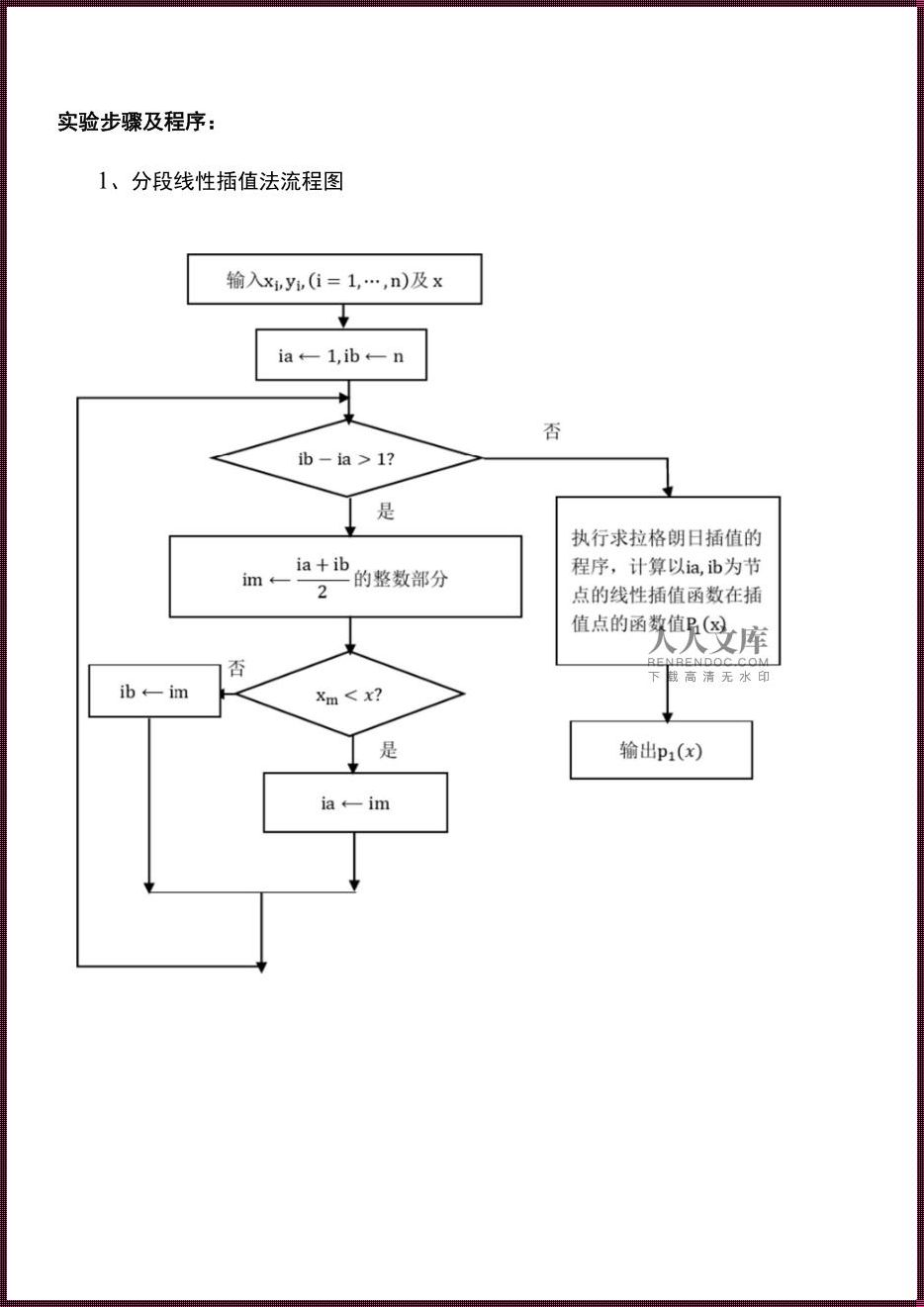
1. 数据收集： 首先，我们需要收集一组数据点，这组数据点由输入的自变量值和对应的函数值组成。这些数据点应当是准确的，因为插值结果的质量直接依赖于这些数据的质量。

2. 选择插值函数： 在三次样条插值中，我们选择三次多项式作为插值函数。三次多项式具有足够的灵活性以拟合数据，同时在整个插值区间内保持连续的二阶导数，这意味着它能够平滑地通过数据点。

3. 构建插值框架： 接下来，我们构建一个插值框架，这个框架由插值节点的横坐标组成。这些节点横坐标的选取可以是任意的，但通常会选择数据点的横坐标作为节点横坐标，以确保数据点本身能够被精确插值。

4. 求解插值系数： 利用所选的插值函数和构建的插值框架，我们通过解一个线性方程组来确定多项式中各个系数的值。这个过程称为“节点插入”，它将确保插值函数通过所有的数据点。

5. 验证和调整： 求解出插值系数后，我们需要验证插值结果是否符合预期的精确度。如果结果不符合要求，我们可能需要返回前面的步骤，重新收集数据或者调整插值框架。

6. 应用和拓展： 一旦我们得到了一个满意的插值函数，我们就可以将它应用到实际的计算中。此外，我们还可以通过拓展数据点的方式来进一步验证插值函数的准确性和适用性。

在这个过程中，精确的数据处理和数学运算至关重要。三次样条插值不仅要求我们对数学原理有深刻的理解，还需要我们具备扎实的编程和计算能力。每一步都需要我们细心地进行检查和调整，以确保最终结果的准确性和可靠性。

通过以上步骤，我们不仅能够得到一个精确的插值函数，而且还能在此基础上进行进一步的分析和计算。三次样条插值在数学、物理、工程和经济等领域都有着广泛的应用，是科学计算中不可或缺的工具之一。