一、链式法则概述

链式法则，又称链式链接法则，是一种数学中的归纳法。它描述了函数复合的性质，揭示了函数之间内在的联系。简单来说，链式法则就是求复合函数的导数。在这个过程中，我们惊现了智慧之光。

二、链式法则的简单例子

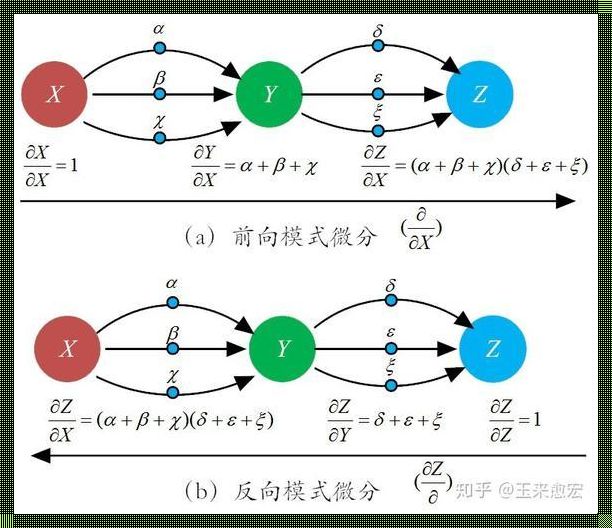
1. 例一：幂函数与指数函数的复合

设函数f(x) = x^n，g(x) = e^x，求复合函数(f ∘ g)(x)。

解析：根据链式法则，(f ∘ g)(x) = e^(x^n)。求导得：(f ∘ g)'(x) = n * x^(n-1) * e^(x^n)。

2. 例二：三角函数与指数函数的复合

设函数f(x) = sin(x)，g(x) = e^x，求复合函数(f ∘ g)(x)。

解析：根据链式法则，(f ∘ g)(x) = e^(x * sin(x))。求导得：(f ∘ g)'(x) = e^(x * sin(x)) * (sin(x) + cos(x))。

三、链式法则的应用

链式法则在数学、物理、工程等领域具有广泛的应用。通过复合函数的求导，我们可以揭示不同函数之间的联系，进一步研究函数的性质。例如，在神经网络中，链式法则用于计算梯度，从而优化模型参数；在经济学中，链式法则可用于分析价格、成本等变量之间的关系。

四、惊现智慧之光

链式法则的运用，让我们在求解复杂问题时，找到了一条路径。这条路径犹如智慧之光，照亮了我们探索未知世界的道路。在这个过程中，我们学会了如何分解问题、如何寻找问题的内在联系。正是这种智慧之光，激发了我们对知识的渴望，引领我们在科学、技术、艺术等各个领域不断前行。

五、结语

链式法则作为一个基本的数学原理，其简单例子揭示了函数之间的联系，为我们解决实际问题提供了有力工具。在这个过程中，我们感受到了智慧之光的力量。正如古人云：“授人以鱼，不如授人以渔。”掌握链式法则，让我们在探索未知的道路上，勇往直前。